��Ŀ����
7��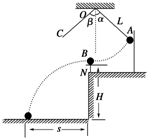 ����ͼ��ʾװ��������̽����ײ�IJ�������ʵ�飬����ΪmB�ĸ���B����С֧��N�ϣ����������߶�ΪH������ΪmA�ĸ���A��ϸ��˩��������O�㣬��ϸ�߱���ֱʱO�㵽���ĵľ���ΪL����ϸ������ֱ��֮��н�Ϊ������A�ɾ�ֹ�ͷţ��ڵ���͵�ʱǡ����B������������ײ��A�������ָʾ��C���Ƶ�����ֱ�н�Ϊ�´���B���䵽�����ϣ�����������һ�Ÿ����и�дֽ�İ�ֽD��������¼��B����㣮���֦��ǶȲ��䣬����ظ�����ʵ�飬�ڰ�ֽ�ϼ�¼�����B�����ص㣮
����ͼ��ʾװ��������̽����ײ�IJ�������ʵ�飬����ΪmB�ĸ���B����С֧��N�ϣ����������߶�ΪH������ΪmA�ĸ���A��ϸ��˩��������O�㣬��ϸ�߱���ֱʱO�㵽���ĵľ���ΪL����ϸ������ֱ��֮��н�Ϊ������A�ɾ�ֹ�ͷţ��ڵ���͵�ʱǡ����B������������ײ��A�������ָʾ��C���Ƶ�����ֱ�н�Ϊ�´���B���䵽�����ϣ�����������һ�Ÿ����и�дֽ�İ�ֽD��������¼��B����㣮���֦��ǶȲ��䣬����ظ�����ʵ�飬�ڰ�ֽ�ϼ�¼�����B�����ص㣮��1��ͼ��sӦ��B���ʼλ�õ�B�������ˮƽ���룮
��2��Ϊ��̽����ײ�е��غ�����Ӧ���mA��mB��L�������¡�H��s����������
��3���ò�õ���������ʾ��mAvA=mA$\sqrt{2gL��1-cos����}$��mAv��A=mA$\sqrt{2gL��1-cos�£�}$��mBv��B=mBS$\sqrt{\frac{g}{2H}}$��
���� A���°ڹ��̻�е���غ㣬�����غ㶨����ʽ����͵��ٶȣ���A�ϰڹ��̻�е���ٴ��غ㣬�������ײ���ٶȣ���ײ��С��B��ƽ���˶�������ƽ���˶��ķ�λ�ƹ�ʽ�����ײ��B����ٶȣ���������ı���ʽ��Ȼ��������⣮
��� �⣺��1����ͼ��֪��SΪB��ij�ʼλ�õ�B������ľ��룻
��2��С���A���°ڹ���ֻ��������������е���غ㣬�ɻ�е���غ㶨�ɵã�
mAgL��1-cos����=$\frac{1}{2}$mAvA2-0��
��ã�vA=$\sqrt{2gL��1-cos����}$��
��PA=mAvA=mA$\sqrt{2gL��1-cos����}$��Ϊ�˲�����ײǰA��Ķ�������Ҫ�������������У�mA������L��
С��A��С��B��ײ������˶�����A��������˹����У���е���ٴ��غ㣬�ɻ�е���غ㶨�ɵã�
-mAgL��1-cos�£�=0-$\frac{1}{2}$mAvA��2��
���vA��=$\sqrt{2gL��1-cos�£�}$��
PA��=mAvA��=mA$\sqrt{2gL��1-cos�£�}$��Ϊ�˲�����ײ��A��Ķ�������Ҫ�������������У�mA���¡�L��
��ǰС��B��ֹ����PB=0��
��ײ��B����ƽ���˶���ˮƽ����S=vB��t����ֱ����H=$\frac{1}{2}$gt2��
��ã�vB��=S$\sqrt{\frac{g}{2H}}$��
������B��Ķ���Ϊ��PB��=mBvB��=mBs$\sqrt{\frac{g}{2H}}$��
Ϊ�˲�����ײ��B��Ķ�������Ҫ�������������У�
�ɶ����غ㶨�ɿ�֪��ʵ����Ҫ������������Ϊ��mA��mB��L�������¡�H��s��
�����ϼ���ɵã��ò�������������ʾ���Ϊ��mAvA=mA$\sqrt{2gL��1-cos����}$��mAv��A=mA$\sqrt{2gL��1-cos�£�}$��mBvB��=mBS$\sqrt{\frac{g}{2H}}$��
�ʴ�Ϊ����1��B����ص㡡��2��mA��mB��L�������¡�H��s
��3��mA$\sqrt{2gL��1-cos����}$��mA$\sqrt{2gL��1-cos�£�}$��mB•s$\sqrt{\frac{g}{2H}}$
���� ���⿼����ȷ��ʵ����Ҫ����������֪��ʵ��ԭ�������ʵ����Ҫ��֤�ı���ʽ����ȷ����Ĺؼ���

 ��ͼ��ʾ�����ڴŸ�Ӧǿ��ΪB����ǿ�ų��еĵ��Ѿ�����Ȧabcd���Ժ㶨�Ľ��ٶȦ���ab��ת�����ų�����ֱ��ֽ�������Ȧ��Χ���ΪS����Ȧ���ߵ��ܵ���ΪR��t=0ʱ����Ȧƽ����ֽ���غϣ���cd������ֽ�����˶���������
��ͼ��ʾ�����ڴŸ�Ӧǿ��ΪB����ǿ�ų��еĵ��Ѿ�����Ȧabcd���Ժ㶨�Ľ��ٶȦ���ab��ת�����ų�����ֱ��ֽ�������Ȧ��Χ���ΪS����Ȧ���ߵ��ܵ���ΪR��t=0ʱ����Ȧƽ����ֽ���غϣ���cd������ֽ�����˶���������| A�� | ʱ��t��Ȧ�е�����˲ʱֵi=$\frac{BS��}{R}$cos��t | |
| B�� | ��Ȧ�е�������ЧֵI=$\frac{BS��}{R}$ | |
| C�� | ��Ȧ�е�������ЧֵI=$\frac{\sqrt{2}BS��}{2R}$ | |
| D�� | ��Ȧ�е����ĵ繦��P=$\frac{��BS�أ�^{2}}{R}$ |
 ��ͼ��ʾ��A������m��B������2m������С��̶���һ������2L����˵����ˣ��˸˿��ƴ��������ĵ�ˮƽ����Ħ����ת������ʹ��˴�ˮƽ״̬���ٵ��ͷţ���˴��ͷ���ת��90��֮��A���ٶ�Ϊ$\sqrt{\frac{2}{3}gL}$����е������$\frac{4}{3}mgL$��
��ͼ��ʾ��A������m��B������2m������С��̶���һ������2L����˵����ˣ��˸˿��ƴ��������ĵ�ˮƽ����Ħ����ת������ʹ��˴�ˮƽ״̬���ٵ��ͷţ���˴��ͷ���ת��90��֮��A���ٶ�Ϊ$\sqrt{\frac{2}{3}gL}$����е������$\frac{4}{3}mgL$�� ��ͼ��ʾ��б��ֱ����Ǵֲڵģ���СԲ����⻬�Ҿ���б��ֱ������У�����СԲ����뾶ΪR���е�ֱ�ΪC��B��Բ�ι���ij���ڴ�������СԲ�������ߵ��б�����ߵ���ͬһˮƽ���ϣ�б��ֱ��������Ϊ60�㣮����һ����Ϊm��С����A�Գ��ٶ�v0��б�滬�£��˶���B�����СԲ�ι������������б���»������Բ�ι���˶���С����б���Ķ�Ħ��������=$\frac{\sqrt{3}}{6}$����
��ͼ��ʾ��б��ֱ����Ǵֲڵģ���СԲ����⻬�Ҿ���б��ֱ������У�����СԲ����뾶ΪR���е�ֱ�ΪC��B��Բ�ι���ij���ڴ�������СԲ�������ߵ��б�����ߵ���ͬһˮƽ���ϣ�б��ֱ��������Ϊ60�㣮����һ����Ϊm��С����A�Գ��ٶ�v0��б�滬�£��˶���B�����СԲ�ι������������б���»������Բ�ι���˶���С����б���Ķ�Ħ��������=$\frac{\sqrt{3}}{6}$����
 ��ͼ��ʾ������ΪN=100�ѵľ�����Ȧabcd����߳�ab=20cm��bc=10cm����Ȧ�ƴ�ֱ����ǿ�ų��������OO������ת����ת��Ϊn=50r/s���Ÿ�Ӧǿ��B=0.1T��ȡ��=3.14����
��ͼ��ʾ������ΪN=100�ѵľ�����Ȧabcd����߳�ab=20cm��bc=10cm����Ȧ�ƴ�ֱ����ǿ�ų��������OO������ת����ת��Ϊn=50r/s���Ÿ�Ӧǿ��B=0.1T��ȡ��=3.14����