题目内容
16.已知某星球的质量是地球质量的81倍,半径是地球半径的9倍.在地球上发射一颗卫星,其第一宇宙速度为7.9km/s,则在某星球上发射一颗人造卫星,其第一宇宙速度是多少?分析 建立模型:卫星绕地球做匀速圆周运动,地球对卫星的万有引力提供向心力.推广到其他球星.根据此模型,利用比例法求星球上发射人造卫星最小发射速度.
解答 解:设地球质量为M1,半径为R1;某星球的质量为M2,半径为R2
由万有引力定律得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
可得:v=$\sqrt{\frac{GM}{R}}$
故地球和该星球第一宇宙速度之比为:$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{M}_{1}{R}_{2}}{{M}_{2}{R}_{1}}}$=$\sqrt{\frac{1×9}{81×1}}$=$\frac{1}{3}$
则在该星球上的第一宇宙速度是为:v2=3v1=23.7km/s
答:某星球上发射一颗人造卫星,其第一宇宙速度是23.7km/s.
点评 本题是卫星类型问题,关键是要建立物理模型,运用万有引力定律和向心力知识,加上数学变换来求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
4.运动员用200N的力把质量为0.5kg的球以速度20m/s踢出,小球在草地上滚了10m后停下,则运动员对球所做的功是( )
| A. | 200J | B. | 2000J | C. | 100J | D. | 无法确定 |
11. 如图所示,两个物体中间用一个不计质量的轻杆相连.A、B两物体质量分别为m1、m2,它们和斜面间的滑动摩擦系数分别为μ1、μ2.当它们在斜面上加速下滑时,关于杆的受力情况,以下说法正确的是( )
如图所示,两个物体中间用一个不计质量的轻杆相连.A、B两物体质量分别为m1、m2,它们和斜面间的滑动摩擦系数分别为μ1、μ2.当它们在斜面上加速下滑时,关于杆的受力情况,以下说法正确的是( )
 如图所示,两个物体中间用一个不计质量的轻杆相连.A、B两物体质量分别为m1、m2,它们和斜面间的滑动摩擦系数分别为μ1、μ2.当它们在斜面上加速下滑时,关于杆的受力情况,以下说法正确的是( )
如图所示,两个物体中间用一个不计质量的轻杆相连.A、B两物体质量分别为m1、m2,它们和斜面间的滑动摩擦系数分别为μ1、μ2.当它们在斜面上加速下滑时,关于杆的受力情况,以下说法正确的是( )| A. | 只要μ1=μ2,则杆的两端既不受拉力也不受压力 | |
| B. | 若μ1=μ2,m1<m2,则杆受到压力 | |
| C. | 若μ1>μ2,m1<m2,则杆一定受到压力 | |
| D. | 若μ1<μ2,m1>m2,则杆受到压力 |
1. 甲、乙两辆汽车沿平直公路从同一地点同时由静止开始向同一方向运动的v-t图象如图所示,则下列说法正确的是( )
甲、乙两辆汽车沿平直公路从同一地点同时由静止开始向同一方向运动的v-t图象如图所示,则下列说法正确的是( )
 甲、乙两辆汽车沿平直公路从同一地点同时由静止开始向同一方向运动的v-t图象如图所示,则下列说法正确的是( )
甲、乙两辆汽车沿平直公路从同一地点同时由静止开始向同一方向运动的v-t图象如图所示,则下列说法正确的是( )| A. | 0~t时间内,甲的平均速度大于乙的平均速度 | |
| B. | 0~2t时间内,甲的平均速度大于乙的平均速度 | |
| C. | t时刻两车再次相遇 | |
| D. | 在t~2t时间内的某时刻,两车相遇 |
8. 如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
 如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )| A. | t=2s | B. | t=3s | C. | h=45 m | D. | h=20m |
5.α粒子散射实验结果表明( )
| A. | 原子中绝大部分是空的 | |
| B. | 原子中全部正电荷都集中在原子核上 | |
| C. | 原子内有中子 | |
| D. | 原子的质量几乎全部都集中在原子核上 |
6.关于感应电流,下列说法中正确的是( )
| A. | 只要闭合电路内有磁通量,闭合电路中就有感应电流产生 | |
| B. | 穿过螺线管的磁通量发生变化时,螺线管内部就一定有感应电流产生 | |
| C. | 线圈不闭合时,即使穿过线圈的磁通量发生变化,线圈中也没有感应电流 | |
| D. | 以上说法都不正确 |
 如图,质量为M=60kg的人和m=40kg箱子,一起以v0=10m/s的速度在光滑水平的冰面上匀速滑行,前进中突然发现前方有一矮墙.为避免撞墙,人将质量m=40kg的箱子水平推向墙,箱子撞墙后以原速率反向弹回,之后人又接住箱子.求人推出箱子的速度至少多大才能在完成一次推接后避免撞墙墙.
如图,质量为M=60kg的人和m=40kg箱子,一起以v0=10m/s的速度在光滑水平的冰面上匀速滑行,前进中突然发现前方有一矮墙.为避免撞墙,人将质量m=40kg的箱子水平推向墙,箱子撞墙后以原速率反向弹回,之后人又接住箱子.求人推出箱子的速度至少多大才能在完成一次推接后避免撞墙墙.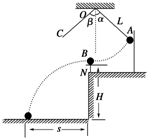 用如图所示装置来进行探究碰撞的不变量的实验,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α.球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张覆盖有复写纸的白纸D,用来记录球B的落点.保持α角度不变,多次重复上述实验,在白纸上记录到多个B球的落地点.
用如图所示装置来进行探究碰撞的不变量的实验,质量为mB的钢球B放在小支柱N上,球心离地面高度为H;质量为mA的钢球A用细线拴好悬挂于O点,当细线被拉直时O点到球心的距离为L,且细线与竖直线之间夹角为α.球A由静止释放,摆到最低点时恰与球B发生正碰,碰撞后,A球把轻质指示针C推移到与竖直线夹角为β处,B球落到地面上,地面上铺有一张覆盖有复写纸的白纸D,用来记录球B的落点.保持α角度不变,多次重复上述实验,在白纸上记录到多个B球的落地点.