题目内容
14.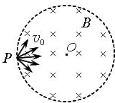 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )| A. | 前后两次粒子运动的轨迹半径比为r1:r2=$\sqrt{2}$:$\sqrt{3}$ | |
| B. | 前后两次粒子运动的轨迹半径比为r1:r2=2:3 | |
| C. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{2}$:$\sqrt{3}$ | |
| D. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{3}$:$\sqrt{2}$ |
分析 当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场,即有圆周上有$\frac{1}{4}$圆弧范围上有粒子射出,找到临界几何条件:即距P点$\frac{1}{4}$圆弧的位置恰好有粒子射出,再与洛伦兹力提供向心力联立即可求出磁感应强度B1和半径r1;
同理,当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场,即有圆周上有$\frac{1}{3}$圆弧的范围上有粒子射出,找到临界几何条件:即距P点$\frac{1}{3}$圆弧的位置恰好有粒子射出,再与洛伦兹力提供向心力联立即可求出磁感应强度B2和半径r2;
解答  解:当磁感应强度为B1时,粒子半径为r1,粒子运动情况如图所示,
解:当磁感应强度为B1时,粒子半径为r1,粒子运动情况如图所示,
根据洛伦兹力提供向心力可得:qv0B1=m$\frac{{v}_{0}^{2}}{{r}_{1}}$…①
根据几何关系有:r1=$\frac{\sqrt{2}}{2}R$…②
联立①②式子可得:B1=$\frac{\sqrt{2}m{v}_{0}}{qR}$…③
当磁感应强度为B2时,粒子半径为r2,粒子运动情况如图所示,
根据洛伦兹力提供向心力可得:qv0B2=m$\frac{{v}_{0}^{2}}{{r}_{2}}$…④
根据几何关系有:r2=$\frac{\sqrt{3}}{2}R$…⑤
联立④⑤式子可得:B2=$\frac{2\sqrt{3}m{v}_{0}}{3qR}$…⑥
由②⑤式可得:前后两次粒子运动的轨迹半径比为r1:r2=$\sqrt{2}$:$\sqrt{3}$,故A正确,B错误;
由③⑥式可得:前后两次磁感应强度的大小之比为B1:B2=$\sqrt{3}$:$\sqrt{2}$,故C错误,D正确;
故选:AD.
点评 本题考查带电粒子在有界磁场中的运动,解题关键是要画出各个方向入射的粒子轨迹过程图,找到临界几何条件,利用洛伦兹力提供向心力结合几何关系求出半径和磁感应强度;本题为定圆的旋转模型,可以找一枚硬币,绕P点旋转观察从圆形磁场区域出射的范围,对数学几何能力要求较高难度较大.


| A. | 图甲的原理和光导纤维传送光信号的原理一样 | |
| B. | 图乙的原理和图丙的原理一样 | |
| C. | 图丙的原理和照相机镜头表面涂上增透膜的原理一样 | |
| D. | 图丁的原理和用标准平面检查光学平面的平整程度的原理一样 |
| A. | 泊松亮斑是光的干涉现象 | |
| B. | 光学镜头上的增透膜是利用光的衍射现象 | |
| C. | 在光导纤维束内传输图象利用了光的全反射原理 | |
| D. | 拍摄玻璃橱窗内的物品时,会在镜头前加装偏振片以增加透射光的强度 |
 奥运会吊环项目中有一个高难度的动作,体操运动员先用双手撑住吊环(设开始时两绳间距与肩同宽),然后身体下移,双臂缓慢张开到如图所示位置.若吊环的两根绳的拉力T大小相等,则在两手之间的距离缓慢增大的过程中,拉力T及其合力F 的大小变化情况为( )
奥运会吊环项目中有一个高难度的动作,体操运动员先用双手撑住吊环(设开始时两绳间距与肩同宽),然后身体下移,双臂缓慢张开到如图所示位置.若吊环的两根绳的拉力T大小相等,则在两手之间的距离缓慢增大的过程中,拉力T及其合力F 的大小变化情况为( )| A. | T增大,F不变 | B. | T增大,F增大 | C. | T增大,F减小 | D. | T减小,F不变 |
 把一个质量m=1kg小球用细线悬挂起来,就成为一个摆,如图所示,摆长l=0.4m,小球从偏角θ=60°的位置由静止释放,摆到悬点的正下方时细线恰好被拉断,此时小球距水平地面的高度h=5m.如果阻力可以忽略,重力加速度g=10m/s2,求:
把一个质量m=1kg小球用细线悬挂起来,就成为一个摆,如图所示,摆长l=0.4m,小球从偏角θ=60°的位置由静止释放,摆到悬点的正下方时细线恰好被拉断,此时小球距水平地面的高度h=5m.如果阻力可以忽略,重力加速度g=10m/s2,求:
 如图所示,一质量为m=0.5kg,边长为L=2.5m的正方形金属线框,放在光滑的水平面上,整个装置放在方向竖直向上,磁感应强度为B=0.8T的有界匀强磁场中,金属线框的一边与磁场的边界MN重合,在水平力F作用下由静止开始向左运动,测得金属线框中的电流随时间变化规律为i=0.1t,经过5s线框被拉出磁场,在金属线框被拉出的过程中.
如图所示,一质量为m=0.5kg,边长为L=2.5m的正方形金属线框,放在光滑的水平面上,整个装置放在方向竖直向上,磁感应强度为B=0.8T的有界匀强磁场中,金属线框的一边与磁场的边界MN重合,在水平力F作用下由静止开始向左运动,测得金属线框中的电流随时间变化规律为i=0.1t,经过5s线框被拉出磁场,在金属线框被拉出的过程中. 如图所示,在直角坐标xoy平面中,第I、IV象限内存在x轴负方向的匀强电场,直线MN与y轴平行,MN与y轴间的两个区域内存在图示垂直于纸面的匀强磁场,磁感应强度大小均为B,x轴为这两个磁场的分界线.图中P点到x轴和y轴的距离分别为(2+$\sqrt{3}$)L和L,现将一质量为m,电荷量为q的带正电的粒子(重力不计)由电场中的P点无初速度释放,粒子经y轴进入磁场后又从y轴上坐标(0,$\sqrt{3}$L)处射出磁场,不计空气阻力.
如图所示,在直角坐标xoy平面中,第I、IV象限内存在x轴负方向的匀强电场,直线MN与y轴平行,MN与y轴间的两个区域内存在图示垂直于纸面的匀强磁场,磁感应强度大小均为B,x轴为这两个磁场的分界线.图中P点到x轴和y轴的距离分别为(2+$\sqrt{3}$)L和L,现将一质量为m,电荷量为q的带正电的粒子(重力不计)由电场中的P点无初速度释放,粒子经y轴进入磁场后又从y轴上坐标(0,$\sqrt{3}$L)处射出磁场,不计空气阻力.