题目内容
6.如图甲所示,一对足够长的平行粗糙导轨固定在水平面上,两导轨间距l=1m,左端之间用R=3Ω的电阻连接,导轨的电阻忽略不计.一根质量m=0.5kg、电阻r=1Ω的导体杆静置于两导轨上,并与两导轨垂直.导体杆到导轨左端的距离为l′=1m.整个装置处于匀强磁场中,磁场方向垂直于导轨平面向上,其大小与时间t的关系如图乙所示,在t=0.5s时,静摩擦力达到最大值,此时施加一水平向右的拉力F拉导体杆,导体杆的v-t图象如丙所示.重力加速度g=10m/s2,设最大静摩擦力等于滑动摩擦力.求:
(1)导体杆与导轨间的动摩擦因数μ以及在0~0.5s内电阻R上产生的热量Q;
(2)拉力F在0.5s~2.5s内与时间t的关系式,并画出其图象.
分析 (1)抓住导体杆在0.5s末开始运动,由法拉第电磁感应定律和欧姆定律求出电流的大小,结合安培力和最大静摩擦力相等求出动摩擦因数.根据焦耳定律求出电阻R上产生的热量.
(2)根据速度时间图线得出匀加速直线运动的加速度,结合牛顿第二定律得出F与t的关系式,从而作出正确的图线.
解答 解:(1)由题意知,当t=0.5s时,导体杆开始运动,
根据法拉第电磁感应定律和欧姆定律得:I=$\frac{△BS}{△t(R+r)}=\frac{△Bll′}{△t(R+r)}$=$4×\frac{1×1}{3+1}A=1A$,
根据BIl=μmg得,动摩擦因数为:μ=$\frac{BIl}{mg}=\frac{2×1×1}{5}=0.4$.
在0-0.5s内通过R的热量为:Q=I2Rt=1×3×0.5J=1.5J.
(2)由导体杆的v-t图象可知,导体杆的加速度为:a=$\frac{4}{2.5-0.5}m/{s}^{2}=2m/{s}^{2}$,
对导体杆,根据牛顿第二定律有:F-μmg-$\frac{{B}^{2}{l}^{2}a(t-0.5)}{R+r}=ma$,
代入数据得:F=2+2t,(t≥0.5s)
其图象如图所示.
答:(1)导体杆与导轨间的动摩擦因数为0.4,在0~0.5s内电阻R上产生的热量为1.5J.
(2)拉力F在0.5s~2.5s内与时间t的关系式为F=2+2t,(t≥0.5s),图象如图所示.
点评 本题考查了电磁感应与图象的综合运用,知道在0-0.5s内产生感生电动势,0.5s后产生动生电动势,掌握法拉第电磁感应定律和闭合电路欧姆定律,并能灵活运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13. 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )| A. | 小球在圆周最低点时速度最大 | |
| B. | 小球在圆周最高点时细绳的拉力最小 | |
| C. | 小球圆周运动过程中细绳的拉力大小不变 | |
| D. | 小球圆周运动时细绳拉力的大小与小球质量无关 |
14.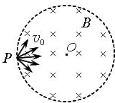 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )| A. | 前后两次粒子运动的轨迹半径比为r1:r2=$\sqrt{2}$:$\sqrt{3}$ | |
| B. | 前后两次粒子运动的轨迹半径比为r1:r2=2:3 | |
| C. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{2}$:$\sqrt{3}$ | |
| D. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{3}$:$\sqrt{2}$ |
1.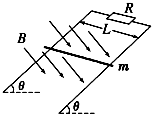 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端接有定值电阻R,匀强磁场垂直于导轨平面,磁感应强度为B.将质量为m的导体棒由静止释放,当速度达到v时开始匀速运动,此时对导体棒施加一平行于导轨向下的拉力,并保持拉力的功率恒为P,导体棒最终以2v的速度匀速运动. 导体棒始终与导轨垂直且接触良好,不计导轨和导体棒的电阻,重力加速度为g.下列选项正确的是( )| A. | P=4mgv sinθ | |
| B. | P=2mgv sinθ | |
| C. | 当导体棒速度为$\frac{v}{2}$时加速度大小为$\frac{g}{2}$sinθ | |
| D. | 在速度达到2v以后匀速运动的过程中,R上产生的焦耳热等于拉力所做的功 |
11.墙上挂着一块长30厘米的平面镜,小明站在镜子前1.5米处,这时他正好可以看到身后的一根木杆,木杆高2米,那么这根木杆离人的距离应该是( )
| A. | 19.5米 | B. | 7.0米 | C. | 10.0米 | D. | 8.5米 |
18. 如图所示,在距离地面某一高度处,沿三个不间的方向分别抛出三个质量和大小均相等的小球,抛出时的速度大小相同,不计空气阻力,则从抛出到落地过程中( )
如图所示,在距离地面某一高度处,沿三个不间的方向分别抛出三个质量和大小均相等的小球,抛出时的速度大小相同,不计空气阻力,则从抛出到落地过程中( )
 如图所示,在距离地面某一高度处,沿三个不间的方向分别抛出三个质量和大小均相等的小球,抛出时的速度大小相同,不计空气阻力,则从抛出到落地过程中( )
如图所示,在距离地面某一高度处,沿三个不间的方向分别抛出三个质量和大小均相等的小球,抛出时的速度大小相同,不计空气阻力,则从抛出到落地过程中( )| A. | 三个小球落地时速度相同 | B. | 三个小球重力做功的平均功率相同 | ||
| C. | 三个小球速度的变化量相同 | D. | 三个小球动能的变化量相同 |
16. 如图所示,一端连接轻弹簧的质量为m的物体B静止在光滑水平面上,质量也为m的物体A以速度v0正对B向右滑行,在A、B和弹簧发生相互作用的过程中,以下判断不正确的是( )
如图所示,一端连接轻弹簧的质量为m的物体B静止在光滑水平面上,质量也为m的物体A以速度v0正对B向右滑行,在A、B和弹簧发生相互作用的过程中,以下判断不正确的是( )
 如图所示,一端连接轻弹簧的质量为m的物体B静止在光滑水平面上,质量也为m的物体A以速度v0正对B向右滑行,在A、B和弹簧发生相互作用的过程中,以下判断不正确的是( )
如图所示,一端连接轻弹簧的质量为m的物体B静止在光滑水平面上,质量也为m的物体A以速度v0正对B向右滑行,在A、B和弹簧发生相互作用的过程中,以下判断不正确的是( )| A. | 任意时刻A、B和弹簧组成的系统总动量都为mv0 | |
| B. | 弹簧压缩到最短时,A、B两物体的速度相等 | |
| C. | 弹簧的最大弹性势能为$\frac{1}{8}$mv02 | |
| D. | 弹簧压缩到最短时,A、B和弹簧组成的系统总动能最小 |

