题目内容
1. 把一个质量m=1kg小球用细线悬挂起来,就成为一个摆,如图所示,摆长l=0.4m,小球从偏角θ=60°的位置由静止释放,摆到悬点的正下方时细线恰好被拉断,此时小球距水平地面的高度h=5m.如果阻力可以忽略,重力加速度g=10m/s2,求:
把一个质量m=1kg小球用细线悬挂起来,就成为一个摆,如图所示,摆长l=0.4m,小球从偏角θ=60°的位置由静止释放,摆到悬点的正下方时细线恰好被拉断,此时小球距水平地面的高度h=5m.如果阻力可以忽略,重力加速度g=10m/s2,求:(1)细线恰好被拉断时小球的速度大小;
(2)小球落地点距P点的距离(P点在悬点的正下方).
分析 (1)根据动能定理求出细线恰好被拉断时小球的速度大小.
(2)根据平抛运动的高度求出小球平抛运动的时间,结合初速度和时间求出小球落地点与P点的距离.
解答 解:(1)小球由静止释放后,受重力、绳的拉力作用,绳的拉力不做功,只有重力做功,设细线恰好被拉断时小球的速度为v,由动能定理可得:$mgl(1-cosθ)=\frac{1}{2}m{v^2}-0$,
代入数据得:v=2 m/s.
(2)小球从摆的最低点开始做平抛运动,设小球落地点距P点的距离为x,由平抛知识得:x=vt
$h=\frac{1}{2}g{t^2}$,
联立代入数据得:x=2m.
答:(1)细线恰好被拉断时小球的速度大小为2m/s;
(2)小球落地点距P点的距离为2m.
点评 本题考查了圆周运动和平抛运动的综合运用,知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式灵活求解.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11. 竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下匀速上升,以下说法正确的是( )
竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下匀速上升,以下说法正确的是( )
 竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下匀速上升,以下说法正确的是( )
竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下匀速上升,以下说法正确的是( )| A. | 作用在金属棒上各力的合力做功为零 | |
| B. | 重力做的功等于系统产生的电能 | |
| C. | 金属棒克服安培力做的功等于电阻R上产生的焦耳热 | |
| D. | 金属棒克服恒力F做的功等于电阻R上产生的焦耳热 |
16.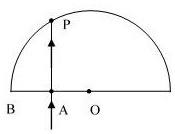 如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
 如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )
如图所示半圆形玻璃砖,圆心为 O,半径为 R.某单色光由空气从 OB 边界的中点 A垂直射入玻璃砖,并在圆弧边界 P 点发生折射,该折射 光线的反向延长线刚好过B点.则( )| A. | 该玻璃对此单色光的折射率为1.5 | |
| B. | 光从 A 传到 P 的时间为$\frac{3R}{2c}$(c为空气中的光速) | |
| C. | 该玻璃对此单色光的临界角为45° | |
| D. | 玻璃的临界角随入射光线位置变化而变化 |
6. 如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )
如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )
 如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )
如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )| A. | 车的速度越大,惯性越大 | |
| B. | 驾驶员系上安全带的目的是为了减少惯性 | |
| C. | 安全带对驾驶员的作用力大于驾驶员对安全带的作用力 | |
| D. | 刹车时,车对地面的摩擦力大小等于地面对车的摩擦力大小 |
13. 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )| A. | 小球在圆周最低点时速度最大 | |
| B. | 小球在圆周最高点时细绳的拉力最小 | |
| C. | 小球圆周运动过程中细绳的拉力大小不变 | |
| D. | 小球圆周运动时细绳拉力的大小与小球质量无关 |
14.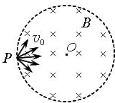 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )| A. | 前后两次粒子运动的轨迹半径比为r1:r2=$\sqrt{2}$:$\sqrt{3}$ | |
| B. | 前后两次粒子运动的轨迹半径比为r1:r2=2:3 | |
| C. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{2}$:$\sqrt{3}$ | |
| D. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{3}$:$\sqrt{2}$ |


