题目内容
2.如图所示,N匝矩形金属线圈的质量为m,电阻为R,放在倾角为θ的光滑斜面上,其ab边长度为L且与斜面底边平行.与ab平行的两水平虚线MN、PQ之间,在t=0时刻加一变化的磁场,磁感应强度B大小随时间t的变化关系为B=kt,方向垂直斜面向上.在t=0时刻将线圈由图中位置静止释放,在t=t1时刻ab边进入磁场,t=t2时刻ab边穿出磁场.线圈ab边刚进入磁场瞬间电流为0,穿出磁场前的瞬间线圈加速度为0.(重力加速度为g)求:
(1)t=t1时刻动生电动势E1的大小和方向;
(2)MN、PQ之间的距离d;
(3)从t=0到t1过程中线圈产生的热量Q;
(4)t=t2时刻线圈的速度v2.
分析 (1)ab边进入磁场前,线圈做匀加速运动,由牛顿第二定律可以求出线圈的加速度,由匀变速运动的速度公式求出ab边进入磁场时的速度;由法拉第电磁定律求出由于磁场变化而产生的感应电动势,由E=BLv求出ab切割磁感线而产生的感应电动势;
(2)由题意知,这两个电动势的和电动势是零,据此求出磁场的宽度d.
(3)由欧姆定律求出感应电流,由焦耳定律求出焦耳热.
(4)线圈穿出磁场时的加速度为零,合力为零,求出此时线圈受到的安培力,由平衡条件求出线圈穿出磁场时的速度.
解答 解:(1)线圈进入磁场前做匀加速运动,
由牛顿第二定律得:mgsinθ=ma,
所以a=gsinθ,
当t=t1时,线圈的速度:v1=at1=gsinθt1
ab边切割磁感线产生的感应电动势:
E1′=NB1lv1=NKlgt12sinθ
由右手定则可知,感应电动势的方向由b指向a.
(2)由法拉第电磁感应定律得,由于磁场变化产生的感应电动势:
E1=N$\frac{△Φ}{△t}$=NS$\frac{△B}{△t}$=Ndl$\frac{K{t}_{1}-0}{{t}_{1}-0}$=NKld,
由题意可知瞬间电流为0,
则:E合=E1-E1′=0
即:NKdl=NKlgt12sinθ,
所以磁场宽度:d=gt12sinθ;
(3)由(2)可知:E1=NKld,感应电流:I=$\frac{{E}_{1}}{R}$=$\frac{NKld}{R}$,
从t=0到t=t1运动过程中线圈产生的热量Q:
$Q={I^2}R{t_1}=\frac{{{N^2}{k^2}{L^2}{g^2}{{sin}^2}θt_1^5}}{R}$;
(4)当t=t2时,由题意知:mgsinθ-NB2I2L=0,
设ab边穿出磁场瞬间的速度为v2,
${ε_2}=N{B_2}L{v_2},{I_2}=\frac{{N{B_2}L{v_2}}}{R}$,
所以:${v_2}=\frac{mgRsinθ}{{{N^2}{k^2}{t^2}{L^2}}}$,
答:(1)t=t1时刻动生电动势E1的大小为NKlgt12sinθ,方向由b指向a;
(2)MN、PQ之间的距离为gt12sinθ;
(3)从t=0到t=t1运动过程中线圈产生的热量为$\frac{{N}^{2}{K}^{2}{L}^{2}{g}^{2}(sinθ)^{2}{t}_{1}^{5}}{R}$;
(4)t=t2时刻线圈的速度是$\frac{mgRsinθ}{{N}^{2}{k}^{2}{t}^{2}{L}^{2}}$.
点评 分析清楚线圈的运动过程、对线圈正确受力分析、熟练应用法拉第电磁感应定律、动能定律是正确解题的关键,本题计算量大,过程较复杂,是一道难题,解题是要细心、认真,否则会出错.

 如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )
如图,汽车在行驶过程中,驾驶员看到前方有紧急情况立即刹车,关于汽车的运动,下列说法正确的是( )| A. | 车的速度越大,惯性越大 | |
| B. | 驾驶员系上安全带的目的是为了减少惯性 | |
| C. | 安全带对驾驶员的作用力大于驾驶员对安全带的作用力 | |
| D. | 刹车时,车对地面的摩擦力大小等于地面对车的摩擦力大小 |
 2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )
2015年7月28日,航天员王亚平在绕地球做匀速圆周运动运动的“天宫一号”里为全国青少年进行太空授课.其中有这样一个实验:在固定的T形支架上,细绳拴着一颗小钢球,王亚平用手指轻推小球,小球绕着T形支架的轴心在竖直平面上做圆周运动,则( )| A. | 小球在圆周最低点时速度最大 | |
| B. | 小球在圆周最高点时细绳的拉力最小 | |
| C. | 小球圆周运动过程中细绳的拉力大小不变 | |
| D. | 小球圆周运动时细绳拉力的大小与小球质量无关 |
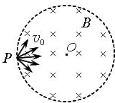 在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )
在半径为R的圆形区域内,存在垂直圆面的匀强磁场.圆边上的P处有一粒子源,不沿垂直于磁场的各个方向,向磁场区发射速率均为v0的同种粒子,如图所示.现测得:当磁感应强度为B1时,粒子均从由P点开始弧长为$\frac{1}{2}πR$的圆周范围内射出磁场;当磁感应强度为B2时,粒子则都从由P点开始弧长为$\frac{2}{3}πR$的圆周范围内射出磁场.不计粒子的重力,则( )| A. | 前后两次粒子运动的轨迹半径比为r1:r2=$\sqrt{2}$:$\sqrt{3}$ | |
| B. | 前后两次粒子运动的轨迹半径比为r1:r2=2:3 | |
| C. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{2}$:$\sqrt{3}$ | |
| D. | 前后两次磁感应强度的大小之比为B1:B2=$\sqrt{3}$:$\sqrt{2}$ |
| A. | 19.5米 | B. | 7.0米 | C. | 10.0米 | D. | 8.5米 |
 甲图为空中溜索,其原理可以简化为乙图,在倾角为θ索道杆上套一个质量为m的圆环,圆环通过轻绳拉着一个质量为M的物块.在圆环沿滑杆向下滑动的某一小段 过程中悬挂物块的轻绳恰好竖直,则此过程中( )
甲图为空中溜索,其原理可以简化为乙图,在倾角为θ索道杆上套一个质量为m的圆环,圆环通过轻绳拉着一个质量为M的物块.在圆环沿滑杆向下滑动的某一小段 过程中悬挂物块的轻绳恰好竖直,则此过程中( )| A. | 物块匀加速下滑 | B. | 环与杆间没有摩擦力 | ||
| C. | 环受到的摩擦力为mgsinθ | D. | 物块受到的拉力为Mg |
 如图所示,两根电阻不计的光滑金属导轨MAC、NBD水平放置,MA、NB间距L=0.4m,AC、BD的延长线相交于E点且AE=BE,E点到AB的距离d=6m,M、N两端与阻值R=2Ω的电阻相连,虚线右侧存在方向与导轨平面垂直向下的匀强磁场,磁感应强度B=1T.一根长度也为L=0.4m、质量m=0.6kg、电阻不计的金属棒,在外力作用下从AB处以初速度v0=2m/s沿导轨水平向右运动,棒与导轨接触良好,运动过程中电阻R上消耗的电功率不变,求:
如图所示,两根电阻不计的光滑金属导轨MAC、NBD水平放置,MA、NB间距L=0.4m,AC、BD的延长线相交于E点且AE=BE,E点到AB的距离d=6m,M、N两端与阻值R=2Ω的电阻相连,虚线右侧存在方向与导轨平面垂直向下的匀强磁场,磁感应强度B=1T.一根长度也为L=0.4m、质量m=0.6kg、电阻不计的金属棒,在外力作用下从AB处以初速度v0=2m/s沿导轨水平向右运动,棒与导轨接触良好,运动过程中电阻R上消耗的电功率不变,求:
 如图所示,导体棒ab长为4L,匀强磁场的磁感应强度为B,导体绕过O点垂直纸面的轴以角速度ω匀速转动,ao=L.则a端和b端的电势差Uab的大小等于4BL2ω.
如图所示,导体棒ab长为4L,匀强磁场的磁感应强度为B,导体绕过O点垂直纸面的轴以角速度ω匀速转动,ao=L.则a端和b端的电势差Uab的大小等于4BL2ω.