题目内容
16.如图甲所示,质量为m=lkg的物体置于倾角为θ=37°固定斜面上(斜面足够长),对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的部分v-t图象如图乙,试求: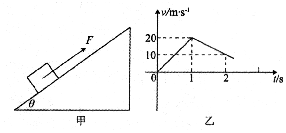
(1)物体与斜面间的滑动摩擦因数;
(2)第ls内拉力F的平均功率;
(3)物体返回原处的时间.
分析 (1)向上做减速运动的过程中,对物体进行受力分析,根据牛顿第二定律列方程求出动摩擦因数;
(2)在向上做加速运动的过程中,对物体进行受力分析,根据牛顿第二定律列方程求出拉力;
(3)由运动学的时间即可求出物体返回原处的时间.
解答 解:(1)设力F作用时物体的加速度为a1,撤去拉力后物体的加速度大小为a2;
根据图象可知:a1=$\frac{20-0}{1}$=20 m/s2,a2=$\frac{20-10}{1}$=10 m/s2
撤去力F后,由牛顿第二定律有mgsinθ+μmgcosθ=ma2
代入数据得:μ=0.5
(2)物体向上加速的过程中,对物体进行受力分析,由牛顿第二定律可知
F-mgsinθ-μmgcosθ=ma1
撤去力F后,由牛顿第二定律有mgsinθ+μmgcosθ=ma2
代入解得F=30 N
由图可知向上加速运动的时间:t1=1s
由图象可知,向上加速运动的过程中的位移:${x}_{1}=\overline{v}{t}_{1}=\frac{0+20}{2}×1=10$m
拉力的平均功率:P=$\frac{F{x}_{1}}{{t}_{1}}=\frac{30×10}{1}=300$W
(3)向上减速的位移:${x}_{2}=\frac{{v}_{m}^{2}}{2{a}_{2}}=\frac{2{0}^{2}}{2×10}=20$m
上滑时的位移x=x1+x2=10m+20m=30m,
向上减速的时间:${t}_{2}=\frac{{v}_{m}}{{a}_{2}}=\frac{20}{10}=2$s
下滑时由牛顿第二定律得:mgsinθ-μmgcosθ=ma3,
又:$x=\frac{1}{2}a{t}_{3}^{2}$
代入数据得:${t}_{3}=\sqrt{30}$s,
故:$t={t}_{1}+{t}_{2}+{t}_{3}=1+2+\sqrt{30}$=3+$\sqrt{30}$(s)
答:(1)物体与斜面间的滑动摩擦因数是0.5;
(2)第ls内拉力F的平均功率是300W;
(3)物体返回原处的时间是(3+$\sqrt{30}$)s.
点评 本题关键受力分析后,根据牛顿第二定律,运用正交分解法求解出各个运动过程的加速度,然后结合运动学公式列式求解.

 阅读快车系列答案
阅读快车系列答案| A. | 前3秒内的位移是6m | B. | 物体的加速度是1.2m/s2 | ||
| C. | 第3秒内的平均速度是1m/s | D. | 3S末的速度是3.6m/s |
| A. | 探测器的线速度v=$\frac{2πR}{T}$ | |
| B. | 探测器的角速度ω=$\frac{2π}{T}$ | |
| C. | 探测器的向心加速度a=G$\frac{m}{(R+h)^{2}}$ | |
| D. | 火星表面重力加速度g=$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$ |

| A. | 若F1和F2大小不变,θ角变大,合力就越小 | |
| B. | 若F1,F2大小分别为4N,7N,它们合力可以为12N | |
| C. | 若把F进行分解可以有多组分力,但每组只能有两个分力 | |
| D. | 质点除了受F1,F2作用,还受到F的作用 |
 如图所示,小朋友在弹性较好的蹦床上跳跃翻腾,尽情嬉耍.在小朋友接触床面向下运动到最低点的过程中,床面对小朋友的弹力做功及小朋友的运动情况是( )
如图所示,小朋友在弹性较好的蹦床上跳跃翻腾,尽情嬉耍.在小朋友接触床面向下运动到最低点的过程中,床面对小朋友的弹力做功及小朋友的运动情况是( )| A. | 弹力先做负功,再做正功,小朋友的动能一直减小 | |
| B. | 弹力先做正功,再做负功,小朋友的动能先增大后减小 | |
| C. | 弹力一直做负功,小朋友的动能一直减小 | |
| D. | 弹力一直做负功,小朋友的动能先增大后减小 |
 如图所示,V1、V2的内阻分别为3000Ω和1500Ω,R1=R2=500Ω,如果保持电压U不变,当S接通后电压表的读数V1、V2关系是( )
如图所示,V1、V2的内阻分别为3000Ω和1500Ω,R1=R2=500Ω,如果保持电压U不变,当S接通后电压表的读数V1、V2关系是( )| A. | V1>V2 | B. | V1=V2 | ||
| C. | V1<V2 | D. | 不能确定V1和V2谁大 |

 林玲同学为了研究磁场对带电粒子辐射的屏蔽作用,设计了如下探究实验:水平放置的矩形屏蔽装置ABCD的AB面为缺口,粒子可从其中射出,其他面为屏蔽面,放射源辐射的带电粒子无法射出,已知AB长x1=20cm,BC长x2=10$\sqrt{3}$cm,在CD的中心O处放置放射源,其能辐射出α、β两种带电射线,其中α粒子的质量m1=6.6×10-27kg,电荷量q1=3.2×10-19C,粒子速率v1=3.2×106m/s;β粒子的质量m2=9.1×10-31kg,电荷量q2=-1.6×10-19C,粒子速率v2=2.7×108m/s.PQ为平行放置在AB上方的探测装置,可以显示辐射到其上的带电粒子,PQ与AB间距为d,整个装置处于真空环境中.
林玲同学为了研究磁场对带电粒子辐射的屏蔽作用,设计了如下探究实验:水平放置的矩形屏蔽装置ABCD的AB面为缺口,粒子可从其中射出,其他面为屏蔽面,放射源辐射的带电粒子无法射出,已知AB长x1=20cm,BC长x2=10$\sqrt{3}$cm,在CD的中心O处放置放射源,其能辐射出α、β两种带电射线,其中α粒子的质量m1=6.6×10-27kg,电荷量q1=3.2×10-19C,粒子速率v1=3.2×106m/s;β粒子的质量m2=9.1×10-31kg,电荷量q2=-1.6×10-19C,粒子速率v2=2.7×108m/s.PQ为平行放置在AB上方的探测装置,可以显示辐射到其上的带电粒子,PQ与AB间距为d,整个装置处于真空环境中.