题目内容
16. 林玲同学为了研究磁场对带电粒子辐射的屏蔽作用,设计了如下探究实验:水平放置的矩形屏蔽装置ABCD的AB面为缺口,粒子可从其中射出,其他面为屏蔽面,放射源辐射的带电粒子无法射出,已知AB长x1=20cm,BC长x2=10$\sqrt{3}$cm,在CD的中心O处放置放射源,其能辐射出α、β两种带电射线,其中α粒子的质量m1=6.6×10-27kg,电荷量q1=3.2×10-19C,粒子速率v1=3.2×106m/s;β粒子的质量m2=9.1×10-31kg,电荷量q2=-1.6×10-19C,粒子速率v2=2.7×108m/s.PQ为平行放置在AB上方的探测装置,可以显示辐射到其上的带电粒子,PQ与AB间距为d,整个装置处于真空环境中.
林玲同学为了研究磁场对带电粒子辐射的屏蔽作用,设计了如下探究实验:水平放置的矩形屏蔽装置ABCD的AB面为缺口,粒子可从其中射出,其他面为屏蔽面,放射源辐射的带电粒子无法射出,已知AB长x1=20cm,BC长x2=10$\sqrt{3}$cm,在CD的中心O处放置放射源,其能辐射出α、β两种带电射线,其中α粒子的质量m1=6.6×10-27kg,电荷量q1=3.2×10-19C,粒子速率v1=3.2×106m/s;β粒子的质量m2=9.1×10-31kg,电荷量q2=-1.6×10-19C,粒子速率v2=2.7×108m/s.PQ为平行放置在AB上方的探测装置,可以显示辐射到其上的带电粒子,PQ与AB间距为d,整个装置处于真空环境中.(1)林玲同学在AB与PQ间加上磁感应强度大小B=0.33T、方向如图所示的匀强磁场,改变PQ与AB的间距,使PQ上恰好探测不到带电粒子,此时PQ与AB的间距d1=30cm.
(2)若AB与PQ间距d2=20cm,则在PQ上带电粒子到达的长度xEF=30cm.
(3)若磁场方向改为垂直纸面向外,上述结论仍成立吗?成立(填“成立”或“不成立”).
(4)为使粒子不能射出磁场,请你提出两条增大磁屏蔽效果的措施.
分析 (1)改变PQ与AB的间距,使PQ上恰好探测不到带电粒子,洛伦兹力提供向心力求出两粒子半径,找到临界情况,即:让最容易打在PQ上的粒子(沿OB方向射出的电子)恰好打不到PQ即可;
(2)洛伦兹力提供向心力与几何关系结合即可;
(3)运用对称性去解决;
(4)根据粒子在磁场中做匀速圆周运动的半径公式结合几何关系,定性分析,合理即可.
解答 
 解:(1)根据洛伦兹力提供向心力:qvB=m$\frac{{v}^{2}}{r}$
解:(1)根据洛伦兹力提供向心力:qvB=m$\frac{{v}^{2}}{r}$
可得:α粒子在磁场中的半径r1=$\frac{{m}_{1}{v}_{1}}{{q}_{1}B}$=$\frac{6.6×1{0}^{-27}×3.2×1{0}^{6}}{3.2×1{0}^{-19}×0.33}$m=0.2m
β粒子在磁场中的半径r2=$\frac{{m}_{2}{v}_{2}}{{q}_{2}B}$=$\frac{9.1×1{0}^{-31}×2.7×1{0}^{8}}{1.6×1{0}^{-19}×0.33}$m≈4.65×10-3m
分析可知只要让沿OA方向射出的α粒子恰好不打到PQ即可,轨迹如图一所示,
根据AD=$\sqrt{3}$OD
所以∠O1AB=∠OAD=30°
根据几何关系有:d=r1(1+sin30°)=0.2×(1+0.5)m=0.3m=30cm
(2)分析可知电子无法打到QP上,如图二所示,从A点射入磁场的α粒子打在QP上最右边的F点,从AB中点入射磁场的α粒子打在QP上最左边的E点
根据几何关系有xEF=r1+$\frac{{x}_{1}}{2}$=0.2m+$\frac{20}{2}$cm=30cm
(3)根据对称性可知:若磁场方向改为垂直纸面向外,沿每个方向入射的两粒子轨迹与原来的轨迹左右对称,故(1)(2)两问的数值不变
(4)根据半径公式r=$\frac{mv}{qB}$可知增大磁感应强度,可使粒子半径r变小,更不易穿出磁场区域;或者增大屏蔽磁场宽度d使磁场区域变大,也可以增大屏蔽效果,使粒子更不易穿出磁场.
故答案为:(1)30; (2)30; (3)成立; (4)增大磁感应强度,增大屏蔽磁场宽度d.
点评 本题考查带电粒子在磁场中的圆周运动,运用洛伦兹力提供向心力结合圆周运动的规律的方法求出半径,再结合几何关系即可,要注意找好临界条件.

 阅读快车系列答案
阅读快车系列答案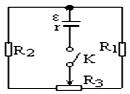 如图所示电路,已知电源电动势E=6.3V,内电阻r=0.5Ω,固定电阻R1=2Ω,R2=3Ω,R3是阻值为5Ω的滑动变阻器.按下电键K,调节滑动变阻器的触点,则通过电源的电流可能是以下哪些值( )
如图所示电路,已知电源电动势E=6.3V,内电阻r=0.5Ω,固定电阻R1=2Ω,R2=3Ω,R3是阻值为5Ω的滑动变阻器.按下电键K,调节滑动变阻器的触点,则通过电源的电流可能是以下哪些值( )| A. | 1.8A | B. | 2.1A | C. | 2.2A | D. | 2.9A |

| A. | 通过细棒的电流比粗棒的大 | |
| B. | 通过细棒的电流比粗棒的小 | |
| C. | 细棒的电阻R1小于粗棒的电阻R2 | |
| D. | 细棒两端的电压U1大于粗棒两端的电压U2 |
| A. | 地球的第一宇宙速度为原来的2倍 | |
| B. | 地球表面的重力加速度变为$\frac{g}{2}$ | |
| C. | 地球的密度变为原来的4倍 | |
| D. | 次仁在地球上以相同的初速度起跳后,能达到的最大高度是$\frac{1}{4}$h |
 电子在电场中运动时,仅受电场力作用,其由a点运动到b点的轨迹如图中虚线所示,图中一组平行等距实线是电场线,则下列说法中正确的是( )
电子在电场中运动时,仅受电场力作用,其由a点运动到b点的轨迹如图中虚线所示,图中一组平行等距实线是电场线,则下列说法中正确的是( )| A. | a点的电势都比b点高 | B. | a点的场强都比b点小 | ||
| C. | 电子由a点运动到b点,动能减小 | D. | 电子由a点运动到b点,电势能减小 |
 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mQ=m的小球连接,另一端与套在光滑直杆上质量mP=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=53°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,(sinθ=0.8,cosθ=0.6)试求:
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mQ=m的小球连接,另一端与套在光滑直杆上质量mP=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=53°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,(sinθ=0.8,cosθ=0.6)试求: 如图所示,光滑绝缘水平直槽上固定着A、B、C三个带电小球,它们的质量均为m,间距均为r,QA=+8q,QB=+q.现对C球施一水平力的同时放开三个小球,欲使三个小球在运动过程中保持间距r不变,求:
如图所示,光滑绝缘水平直槽上固定着A、B、C三个带电小球,它们的质量均为m,间距均为r,QA=+8q,QB=+q.现对C球施一水平力的同时放开三个小球,欲使三个小球在运动过程中保持间距r不变,求: