题目内容
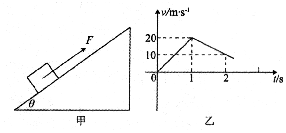
8.质量为2kg的物体,在一平面上受到一个与水平面成37°角的拉力F作用,从静止开始运动,在头4s内通过1.6m的位移.问:(1)拉力F多大?
(2)如果在4s末突然将力F的方向改为水平,大小不变,则6s末物体的速度多大?
(3)在6s内物体运动的总位移多大?
分析 (1)根据位移时间关系可得加速度,根据牛顿第二定律可得拉力大小;
(2)求出4s后的加速度和4s时的速度,根据速度时间关系求解6s末物体的速度;
(3)根据位移时间关系求解后2s的位移,最后求解出6s内物体运动的总位移.
解答 解:(1)根据位移时间关系可得:${x}_{1}=\frac{1}{2}{a}_{1}{t}_{1}^{2}$,
解得加速度:${a}_{1}=\frac{2{x}_{1}}{{t}_{1}^{2}}=\frac{2×1.6}{16}m/{s}^{2}=0.2m/{s}^{2}$.
根据牛顿第二定律可得:Fcos37°=ma1,
解得:F=0.5N;
(2)4s末突然将力F的方向改为水平,加速度为:${a}_{2}=\frac{F}{m}=\frac{0.5}{2}m/{s}^{2}=0.25m/{s}^{2}$,
4s末的速度为:v1=a1t1=0.2×4m/s=0.8m/s,
6s末的速度为:v2=v1+a2t2=(0.8+0.25×2)m/s=1.3m/s;
(3)后2s的位移为x2=$\frac{{v}_{1}+{v}_{2}}{2}{t}_{2}=\frac{0.8+1.3}{2}×2m=2.1m$,
所以6s内物体运动的总位移为x=x1+x2=1.6m+2.1m=3.7m.
答:(1)拉力F为0.5N;
(2)如果在4s末突然将力F的方向改为水平,大小不变,则6s末物体的速度为1.3m/s;
(3)在6s内物体运动的总位移为3.7m.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

练习册系列答案
相关题目
18.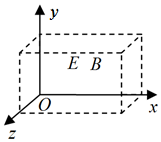 在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
 在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )
在图中虚线所示的区域存在匀强电场和匀强磁场,取坐标如图.一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转.不计重力影响,电场强度E和磁场强度B的方向可能是( )| A. | E和B都沿x轴方向 | B. | E沿y轴正向,B沿z轴正向 | ||
| C. | E沿z轴正向,B沿y轴正向 | D. | E沿z轴正向,B沿y轴负向 |
19.质点做直线运动的v-t图象如图所示,该质点( )
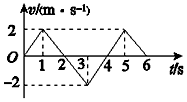

| A. | 在第2秒末加速度方向发生了改变 | B. | 在第2秒末速度方向发生了改变 | ||
| C. | 第3秒末和第5秒末的位置相同 | D. | 在前2秒内发生的位移为零 |
4.如图所示,两个截面不同,长度相等的均匀铜棒接在电路中,两端电压为U,则( )


| A. | 通过细棒的电流比粗棒的大 | |
| B. | 通过细棒的电流比粗棒的小 | |
| C. | 细棒的电阻R1小于粗棒的电阻R2 | |
| D. | 细棒两端的电压U1大于粗棒两端的电压U2 |
9.一个质点做变速直线运动,其运动情况有如下记录,则记录中表示瞬时速度的有( )
| A. | 质点在前5s内的速度是8 m/s | |
| B. | 质点在第7s末的速度是12 m/s | |
| C. | 质点通过某一路标时的速度是15 m/s | |
| D. | 质点通过某一路段的速度为10 m/s |

 如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mQ=m的小球连接,另一端与套在光滑直杆上质量mP=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=53°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,(sinθ=0.8,cosθ=0.6)试求:
如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mQ=m的小球连接,另一端与套在光滑直杆上质量mP=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=53°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,(sinθ=0.8,cosθ=0.6)试求: