题目内容
7.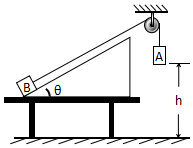 如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)A物体着时的速度大小
(2)为使B物体不从斜面顶端滑出,斜面长至少要多少?
分析 (1)A下落过程,对AB整体应用动能定理求解;
(2)分析A落地后B的受力情况,由动能定理求得B上滑的位移,即可得到B上滑的总位移,进而得到斜面长的最小值.
解答 解:(1)AB通过绳子作用,在A下落过程速度、位移始终一致;那么对A、B整体,根据动能定理得:
$mgh-Mghsinθ-μMghcosθ=\frac{1}{2}(M+m){v}^{2}$;
所以,A物体着时的速度大小为:
$v=\sqrt{\frac{2gh(m-Msinθ-μMcosθ)}{M+m}}=2\sqrt{2}m/s$;
(2)A落地后,B继续沿斜面上滑,此过程中绳子弹力为零,对B,只有重力、摩擦力做功,故根据动能定理可得:
$-Mgssinθ-μMgscosθ=0-\frac{1}{2}M{v}^{2}$;
所以,该过程物体B上滑的位移为:
$s=\frac{{v}^{2}}{2g(sinθ+μcosθ)}=0.5m$;
所以,物体B在斜面上滑动的最大位移为S=h+s=2.5m,那么,为使B物体不从斜面顶端滑出,斜面长至少要2.5m;
答:(1)A物体着时的速度大小为$2\sqrt{2}m/s$;
(2)为使B物体不从斜面顶端滑出,斜面长至少要2.5m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
20. 物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
 物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )| A. | 物块的质量 | |
| B. | 物块与桌面之间的动摩擦因数 | |
| C. | 水平拉力大小 | |
| D. | 物块在前0~2m和后2m~4m内的加速度 |
18.如图所示是一个常用的电子元件,该电子元件 ( )


| A. | 是电阻 | B. | 电容是1000μF | C. | 带电量是16000C | D. | 击穿电压为16V |
13. 如图,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
 如图,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率v1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率v2(v2>v1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )| A. | 滑块返回传送带右端的速率为v1 | |
| B. | 此过程中传送带对滑块做功为$\frac{1}{2}$mv12-$\frac{1}{2}$mv22 | |
| C. | 此过程中电动机对传送带做功为2mv | |
| D. | 此过程中滑块与传送带间摩擦产生的热量为$\frac{1}{2}$m(v12+v2)2 |
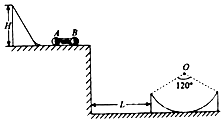 如图所示,小球A和B质量为mA=0.3kg和mB=0.5kg,两球间压缩一弹簧(不栓接),并用细线连接,静止于一光滑的平台上,烧断细线后A球滑上用一小段圆弧连接的光滑斜面,当滑到斜面顶端时速度刚好为零,斜面的高度H=1.25m,B球滑出平台后刚好沿右侧光滑圆槽顶端的切线方向进入槽中,圆形槽的半径R=3m,圆形槽所对的圆心角为120°,g=10m/s2,求:
如图所示,小球A和B质量为mA=0.3kg和mB=0.5kg,两球间压缩一弹簧(不栓接),并用细线连接,静止于一光滑的平台上,烧断细线后A球滑上用一小段圆弧连接的光滑斜面,当滑到斜面顶端时速度刚好为零,斜面的高度H=1.25m,B球滑出平台后刚好沿右侧光滑圆槽顶端的切线方向进入槽中,圆形槽的半径R=3m,圆形槽所对的圆心角为120°,g=10m/s2,求:
 如图所示,倾角θ=37°、长L=4m的斜面,底端与一个光滑的四分之一圆弧轨道平滑连接,圆弧轨道底端切线水平.一质量为m=2kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点.已知物块与斜面间的动摩擦因数为μ=0.3,g=10m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变.求:
如图所示,倾角θ=37°、长L=4m的斜面,底端与一个光滑的四分之一圆弧轨道平滑连接,圆弧轨道底端切线水平.一质量为m=2kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点.已知物块与斜面间的动摩擦因数为μ=0.3,g=10m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变.求: 如图,气缸固定于水平面,用截面积为20cm2的活塞封闭一定量的气体,活塞与缸壁间摩擦不计.当大气压强为1.0×105Pa、气体温度为87℃时,活塞在大小为40N、方向向左的力F作用下保持静止,气体压强为1.2×105Pa.若保持话塞不动,将气体温度降至27℃,则F变为0N.
如图,气缸固定于水平面,用截面积为20cm2的活塞封闭一定量的气体,活塞与缸壁间摩擦不计.当大气压强为1.0×105Pa、气体温度为87℃时,活塞在大小为40N、方向向左的力F作用下保持静止,气体压强为1.2×105Pa.若保持话塞不动,将气体温度降至27℃,则F变为0N.