题目内容
19. 如图所示,倾角θ=37°、长L=4m的斜面,底端与一个光滑的四分之一圆弧轨道平滑连接,圆弧轨道底端切线水平.一质量为m=2kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点.已知物块与斜面间的动摩擦因数为μ=0.3,g=10m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变.求:
如图所示,倾角θ=37°、长L=4m的斜面,底端与一个光滑的四分之一圆弧轨道平滑连接,圆弧轨道底端切线水平.一质量为m=2kg的物块(可视为质点)从斜面最高点A由静止开始沿斜面下滑,经过斜面底端B后恰好能到达圆弧轨道最高点C,又从圆弧轨道滑回,能上升到斜面上的D点,再由D点由斜面下滑沿圆弧轨道上升,再滑回,这样往复运动,最后停在B点.已知物块与斜面间的动摩擦因数为μ=0.3,g=10m/s2,假设物块经过斜面与圆弧轨道平滑连接处速率不变.求:(1)物块第一次经过B点时对圆弧轨道的压力;
(2)物块在斜面上滑行的总路程.
分析 (1)对BC运动过程应用机械能守恒求得在B点的速度,然后由牛顿第二定律求得支持力,即可由牛顿第三定律求得压力;
(2)对整个运动过程应用动能定理求解.
解答 解:(1)物块恰好能到达C点,故物块到C点速度为0,设物块到B点的速度为v,物块从B到C的运动过程只有重力做功,机械能守恒,故有$mgR=\frac{1}{2}m{v}^{2}$;
对物块在B点应用牛顿第二定律可得:物块受到的支持力${F}_{N}=mg+\frac{m{v}^{2}}{R}=3mg=60N$,方向竖直向上;
那么由牛顿第三定律可得:物块第一次经过B点时对圆弧轨道的压力为60N,方向竖直向下;
(2)从开始释放至最终停在B处,只有重力、摩擦力做功;设物块在斜面上滑行的总路程为s,则由动能定理可得:mgLsin θ-μmgscos θ=0
所以,$s=\frac{Lsinθ}{μcosθ}=10m$;
答:(1)物块第一次经过B点时对圆弧轨道的压力为60N,方向竖直向下;
(2)物块在斜面上滑行的总路程为10m.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
12.有关电容器的单位及换算正确的是 ( )
| A. | 电容的单位是库仑 | B. | 电容的国际单位是法拉 | ||
| C. | 法拉是一个很小的单位 | D. | 1μF=l×10-6 F |
13.关于磁感线的概念和性质,下列说法中正确的是( )
| A. | 磁感线上各点的切线方向就是各点的磁感应强度的方向 | |
| B. | 磁感线是磁场中客观存在的曲线 | |
| C. | 铁屑在磁场中分布所形成的曲线就是磁感线 | |
| D. | 磁感线总是从磁体N极出发指向磁体的S极 |
14. 如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )
如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )
 如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )
如图所示,在斯特林循环的P-V图象中,一定质量理想气体从状态a依次经过状态b、c和d后再回到状态a,整个过程由两个等温和两个等容过程组成.下列说法正确的是( )| A. | 从a到b,气体得温度一直升高 | |
| B. | 从b到c,气体与外界无热量交换 | |
| C. | 从c到d,气体对外放热 | |
| D. | 从d到a,单位体积中的气体分子数目增大 | |
| E. | 从b到c气体吸收得热量与从d到a气体气体放出得热量相同 |
11.用起重机将质量相同的物体,从地面匀速提升相同的高度,提升的速率分别为v1和v2,且v1≠v2,那么起重机在两次提升过程中( )
| A. | 速度大的绳的拉力大 | B. | 所需时间相同 | ||
| C. | 功率一样大 | D. | 做的功一样多 |
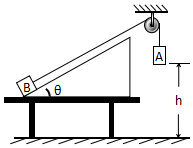 如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,倾角θ=37°的斜面体固定在水平桌面上,质量M=2.0kg的物体B放在斜面底端,与斜面间的动摩擦因数μ=0.25,现通过轻细绳跨过光滑的定滑轮与质量m=2.5kg的A物体相连接,连接B的细绳与斜面平行.若用手托住A物体,使其在距地面h=2m高处由静止释放,A物体着地后立即停止运动,A、B物体均可视为质点,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: 如图所示,两条足够长的光滑平行金属导轨相距为L,与水平面之间的夹角为θ,在整个区域都有垂直于导轨平面斜向上的磁感应强度大小为B的匀强磁场,在接近导轨底端附近导轨上放置一质量为m的导体棒MN,导体棒中点O通过一绝缘轻杆与固定在斜面底端的拉力传感器连接,轻杆与MN垂直,且与导轨平面平行,在导体棒MN上方有一始终与导轨垂直且接触良好的导体棒PQ,现给导体棒PQ一方向沿导轨平面向上的足够大的瞬时冲量I0(此时导体棒MN受到的安培力大于2mgsinθ),使导体棒PQ沿斜面向上运动,已知两导体棒的电阻均为R,导轨的电阻不计,重力加速度为g.
如图所示,两条足够长的光滑平行金属导轨相距为L,与水平面之间的夹角为θ,在整个区域都有垂直于导轨平面斜向上的磁感应强度大小为B的匀强磁场,在接近导轨底端附近导轨上放置一质量为m的导体棒MN,导体棒中点O通过一绝缘轻杆与固定在斜面底端的拉力传感器连接,轻杆与MN垂直,且与导轨平面平行,在导体棒MN上方有一始终与导轨垂直且接触良好的导体棒PQ,现给导体棒PQ一方向沿导轨平面向上的足够大的瞬时冲量I0(此时导体棒MN受到的安培力大于2mgsinθ),使导体棒PQ沿斜面向上运动,已知两导体棒的电阻均为R,导轨的电阻不计,重力加速度为g. 如图所示,A为带正电Q的金属板,沿金属板的垂直平分线,在距板r处放一质量为m、电荷量为q的小球,小球受水平向右的电场力偏转θ角而静止,小球用绝缘丝线悬挂于O点,试求:
如图所示,A为带正电Q的金属板,沿金属板的垂直平分线,在距板r处放一质量为m、电荷量为q的小球,小球受水平向右的电场力偏转θ角而静止,小球用绝缘丝线悬挂于O点,试求: 如图所示,一个质量m=2.0kg的物体,放在倾角a=37°的斜面上静止不动,现用平行斜面向上、大小为30N的力F使物体开始沿斜面向上匀加速运动,在2s内物体的位移为10m.已知物体与斜面之间的动摩擦因数μ=0.5,斜面足够长,重力加速度g=10m/s2,sin37°=0.6,cos37°=038,求:
如图所示,一个质量m=2.0kg的物体,放在倾角a=37°的斜面上静止不动,现用平行斜面向上、大小为30N的力F使物体开始沿斜面向上匀加速运动,在2s内物体的位移为10m.已知物体与斜面之间的动摩擦因数μ=0.5,斜面足够长,重力加速度g=10m/s2,sin37°=0.6,cos37°=038,求: