题目内容
17. 如图1所示,一水平放置的平行板电容器,上极板接地,下极板是一个金属盘,极板长L,两板间的距离d,电容器的电容C,开始电容器不带电.现在平行板电容器的左侧以相同的速度不断地沿平行于极板的方向向右发射质量m、电荷量q的带正电的小液滴,己知落在下极板的小液滴电荷全部被下极板吸收,重力加速度为g,不计小液滴在运动过程中受到的空气阻力和液滴间的作用,不计下极板边缘的高度和由于下极板聚集液体电容器电容的变化.
如图1所示,一水平放置的平行板电容器,上极板接地,下极板是一个金属盘,极板长L,两板间的距离d,电容器的电容C,开始电容器不带电.现在平行板电容器的左侧以相同的速度不断地沿平行于极板的方向向右发射质量m、电荷量q的带正电的小液滴,己知落在下极板的小液滴电荷全部被下极板吸收,重力加速度为g,不计小液滴在运动过程中受到的空气阻力和液滴间的作用,不计下极板边缘的高度和由于下极板聚集液体电容器电容的变化.(1)若小液滴仅从两板间的中心处射入,且已知射入的第一滴小液滴落在下极板的中心,求:①小液滴射入的初速度v0的大小;②最终下极板能收集到的液滴数.
(2)若在两极板间接一直流电源(内阻不计),并使小液滴以(1)中同样大小的速度v0从两板间的各个位置均匀射入(如图2),通过调整电源的输出电压U,可以改变打到下极板的滴数与射入板间总液滴数的比值k.请推导出k随U变化的函数关系式.
分析 (1)根据粒子做平抛运动的规律,运用运动的合成与分解,并依据运动学公式,即可求解;
(2)根据牛顿第二定律,结合电场力表达式,与运动学公式,即可求解.
解答 解:(1)因为开始电容器不带电,射入的第一滴小液滴做平抛运动
水平方向:$\frac{L}{2}={v}_{0}^{\;}t①$
竖直方向:$\frac{d}{2}=\frac{1}{2}g{t}_{\;}^{2}②$
联立得${v}_{0}^{\;}=\frac{L}{2}\sqrt{\frac{g}{d}}$
设最终下极板收集到的液滴数为n
对第(n+1)滴液滴受力平衡mg=qE
$E=\frac{U}{d}$
Q=CU
液滴个数$n=\frac{Q}{q}$
联立得$n=\frac{mgCd}{{q}_{\;}^{2}}$
(2)接直流电源时,U不变
$y=\frac{1}{2}a{t}_{\;}^{2}$
$a=\frac{qE}{m}$
$E=\frac{U}{d}$
$k=\frac{y}{d}$
联立以上各式得:$k=\frac{q{L}_{\;}^{2}U}{2m{d}_{\;}^{2}{v}_{0}^{2}}$
答:(1)若小液滴仅从两板间的中心处射入,且已知射入的第一滴小液滴落在下极板的中心,①小液滴射入的初速度v0的大小$\frac{L}{2}\sqrt{\frac{g}{d}}$;②最终下极板能收集到的液滴数$\frac{mgCd}{{q}_{\;}^{2}}$.
(2)若在两极板间接一直流电源(内阻不计),并使小液滴以(1)中同样大小的速度v0从两板间的各个位置均匀射入(如图2),通过调整电源的输出电压U,可以改变打到下极板的滴数与射入板间总液滴数的比值k.请推导出k随U变化的函数关系式$k=\frac{q{L}_{\;}^{2}U}{2m{d}_{\;}^{2}{v}_{0}^{2}}$.
点评 考查如何处理平抛运动的思路,掌握运动的合成与分解的方法,理解运动学公式与牛顿第二定律的综合应用.

 2015年世界举重锦标赛于11月20日至29日在美国休斯敦举行.如图所示为我国选手邓薇比赛时的画面,若邓薇所举杠铃的质量为m,杠铃平衡时每只手臂与竖直线所成的夹角均为45°.则她每只手臂承受的作用力为( )
2015年世界举重锦标赛于11月20日至29日在美国休斯敦举行.如图所示为我国选手邓薇比赛时的画面,若邓薇所举杠铃的质量为m,杠铃平衡时每只手臂与竖直线所成的夹角均为45°.则她每只手臂承受的作用力为( )| A. | $\frac{\sqrt{3}}{3}$mg | B. | $\frac{1}{2}$mg | C. | $\frac{\sqrt{2}}{2}$mg | D. | mg |
 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,现给小球A一个水平向右的恒力F=50N,g取10m/s2,则下列判断正确的是
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,现给小球A一个水平向右的恒力F=50N,g取10m/s2,则下列判断正确的是( )
| A. | 小球B运动到P的正下方C处的速度大小为0 | |
| B. | 把小球B从地面拉到P的正下方C点力F做功为20J | |
| C. | 小球B被拉到与小球A速度大小相等时,sin∠OPB=$\frac{3}{4}$ | |
| D. | 把小球B从地面拉到P的正下方C点小球B的机械能增加了6J |
| A. | 在单缝衍射实验中,假设只让一个光子通过单缝,则该光子不可能落在暗条纹处 | |
| B. | 质量数大的原子核,其比结合能一定大 | |
| C. | 通过对α粒子散射实验现象的分析,可估算出原子的大小 | |
| D. | 光和运动电子都具有波粒二象性 |
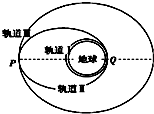 在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )
在发射一颗质量为m的人造地球同步卫星时,先将其发射到贴近地球表面运行的圆轨道Ⅰ上(离地面高度忽略不计),再通过一椭圆轨道Ⅱ变轨后到达距地面高为h的预定圆轨道Ⅲ上.已知它在圆形轨道Ⅰ上运行的加速度为g,地球半径为R,卫星在变轨过程中质量不变,则( )| A. | 卫星在轨道Ⅲ上运行的加速度为($\frac{h}{R+h}$)2g | |
| B. | 卫星在轨道Ⅲ上运行的线速度为v=$\sqrt{\frac{g{R}^{2}}{R+h}}$ | |
| C. | 卫星在轨道Ⅲ上运行时经过P点的速率等于在轨道Ⅱ上运行时经过P点的速率 | |
| D. | 卫星在轨道Ⅲ上的机械能小于在轨道Ⅰ上的机械能 |

| A. | 图甲中电流的峰值为2A,有效值为2.5$\sqrt{2}$ A,周期为5s | |
| B. | 图乙中电流的峰值为5A,有效值为2.5A | |
| C. | 图丙中电流的峰值为2A,有效值为 1A | |
| D. | 图丁中电流的最大值为4A,有效值为 $\sqrt{13.5}$A,周期为2s |
 某同学探究功和动能变化的关系,装置如图所示.
某同学探究功和动能变化的关系,装置如图所示. 如图倾斜的玻璃管长为L=58cm.一端封闭、另一端开口向上,倾角θ=30°.有8cm长的水银柱封闭着45cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg.求:
如图倾斜的玻璃管长为L=58cm.一端封闭、另一端开口向上,倾角θ=30°.有8cm长的水银柱封闭着45cm长的理想气体,管内外气体的温度均为33℃,大气压强p0=76cmHg.求: