题目内容
1.在一次交通事故中,质量为M的货车与静止于前方质量为m的小汽车追尾并推着小汽车向前滑行,交警测得碰撞前货车刹车滑行的距离为x1,碰撞后共同向前滑行的距离为x2,若货车刹车后及与小汽车碰后的运动过程中,货车和小汽车所受阻力均为自身重力的μ倍,求货车刹车前的速度大小.分析 对货车与小汽车碰撞前,根据动能定理列表达式
货车与小汽车碰撞过程,根据动量守恒定律求出两车相撞前后的速度关系,然后对系统根据动能定理列式,从而联立方程即可求解.
解答 解:设碰前货车的速度为 v0,碰后货车速度为v1,则
货车与小汽车碰撞前,对货车据动能定理得:$-μMg{x_1}=\frac{1}{2}Mv_1^2-\frac{1}{2}Mv_0^2$ ①
货车与小汽车碰撞过程,碰后共同速度为v2
根据动量守恒:Mv1=(M+m)v2 ②
两车碰撞后,对货车和小汽车组成的系统,据动能定理得:$-μ(M+m)g{x_2}=0-\frac{1}{2}(M+m)v_2^2$③
解得:${v_0}=\sqrt{2μg{x_1}+\frac{{2{{(M+m)}^2}μg{x_2}}}{M^2}}$④
答:货车刹车前的速度大小为 $\sqrt{2μg{x}_{1}+\frac{2(M+m)^{2}μg{x}_{2}}{{M}^{2}}}$
点评 本题属于中等难度的试题,物理过程清晰,规律应用明确,多数学生能够写出碰撞过程的动量守恒定律的表达式,大量的学生习惯用动力学方法进行求解,而少有应用动能定理进行求解.一些学生在写方程时,过程量(功)与状态量(动能)不对应,说明对象选取不正确,还有部分学生虽然写对方程,但不能正确求解,推理运算的能力太差,十分可惜丢了不该丢的分

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
11. 传感器是把非电学量(如速度、温度、压力等)的变化转换成电学变化的一种元件,在自动控制中有着相当广泛的应用,如图所示是一种测量液面高度的电容式传感器的示意图,金属芯线与导电液体之间形成一个电容器,从电容大小的变化就能反映液面的升降情况.当测得电容值增大,可以确定h将( )
传感器是把非电学量(如速度、温度、压力等)的变化转换成电学变化的一种元件,在自动控制中有着相当广泛的应用,如图所示是一种测量液面高度的电容式传感器的示意图,金属芯线与导电液体之间形成一个电容器,从电容大小的变化就能反映液面的升降情况.当测得电容值增大,可以确定h将( )
 传感器是把非电学量(如速度、温度、压力等)的变化转换成电学变化的一种元件,在自动控制中有着相当广泛的应用,如图所示是一种测量液面高度的电容式传感器的示意图,金属芯线与导电液体之间形成一个电容器,从电容大小的变化就能反映液面的升降情况.当测得电容值增大,可以确定h将( )
传感器是把非电学量(如速度、温度、压力等)的变化转换成电学变化的一种元件,在自动控制中有着相当广泛的应用,如图所示是一种测量液面高度的电容式传感器的示意图,金属芯线与导电液体之间形成一个电容器,从电容大小的变化就能反映液面的升降情况.当测得电容值增大,可以确定h将( )| A. | 减小 | B. | 增大 | C. | 不变 | D. | 无法判断 |
12. 如图为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,P为0.9m处的质点,Q为2.2m处的质点.若经历△t=0.1s,P质点恰好第一次运动到波谷,则下列说法正确的是( )
如图为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,P为0.9m处的质点,Q为2.2m处的质点.若经历△t=0.1s,P质点恰好第一次运动到波谷,则下列说法正确的是( )
 如图为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,P为0.9m处的质点,Q为2.2m处的质点.若经历△t=0.1s,P质点恰好第一次运动到波谷,则下列说法正确的是( )
如图为一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,P为0.9m处的质点,Q为2.2m处的质点.若经历△t=0.1s,P质点恰好第一次运动到波谷,则下列说法正确的是( )| A. | 该波的周期T=0.125s | |
| B. | 该波的传播速度为v=14m/s | |
| C. | 从t=0时刻再经历1s,P质点向前传播的距离为14m | |
| D. | 从t=0时刻再经历0.052s,Q质点一定向上振动 |
9.在研究电场和磁场时,用公式E=$\frac{F}{q}$定义电场强度,用公式B=$\frac{F}{IL}$定义磁感应强度.则下列说法正确的是( )
| A. | E=$\frac{F}{q}$中,q为产生该电场的电荷 | |
| B. | E=$\frac{F}{q}$只适用于点电荷产生的电场 | |
| C. | B=$\frac{F}{IL}$表明磁感应强度B与电流I的大小成反比 | |
| D. | B=$\frac{F}{IL}$中磁感应强度B与电流I、导线长度L均无关 |
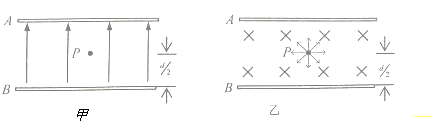
10. 如图所示,无限长且相距为d的竖直边界MN和PQ间充满匀强磁场,磁感应强度方向垂直纸面向里,大小为B,在磁场边界MN上的A处有一粒子源,可以在纸面内向各个方向发射质量为m,电荷量为q,速度大小为v,不计重力的同种粒子,这些粒子都不能到达磁场另一边界PQ的右测,则下列说法正确的是( )
如图所示,无限长且相距为d的竖直边界MN和PQ间充满匀强磁场,磁感应强度方向垂直纸面向里,大小为B,在磁场边界MN上的A处有一粒子源,可以在纸面内向各个方向发射质量为m,电荷量为q,速度大小为v,不计重力的同种粒子,这些粒子都不能到达磁场另一边界PQ的右测,则下列说法正确的是( )
 如图所示,无限长且相距为d的竖直边界MN和PQ间充满匀强磁场,磁感应强度方向垂直纸面向里,大小为B,在磁场边界MN上的A处有一粒子源,可以在纸面内向各个方向发射质量为m,电荷量为q,速度大小为v,不计重力的同种粒子,这些粒子都不能到达磁场另一边界PQ的右测,则下列说法正确的是( )
如图所示,无限长且相距为d的竖直边界MN和PQ间充满匀强磁场,磁感应强度方向垂直纸面向里,大小为B,在磁场边界MN上的A处有一粒子源,可以在纸面内向各个方向发射质量为m,电荷量为q,速度大小为v,不计重力的同种粒子,这些粒子都不能到达磁场另一边界PQ的右测,则下列说法正确的是( )| A. | 所有粒子的速度不超过$\frac{qdB}{2m}$ | |
| B. | 所有粒子的速度不超过 $\frac{qdB}{m}$ | |
| C. | 在边界MN上有粒子射出磁场区域的最大长度为d | |
| D. | 在边界MN上有粒子射出磁场区域的最大长度为2d |
18. 如图所示,三个重均为100N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20N用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20N的小球P.整个装置处于静止状态.则( )
如图所示,三个重均为100N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20N用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20N的小球P.整个装置处于静止状态.则( )
 如图所示,三个重均为100N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20N用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20N的小球P.整个装置处于静止状态.则( )
如图所示,三个重均为100N的物块,叠放在水平桌面上,各接触面水平,水平拉力F=20N用在物块2上,三条轻质绳结于O点,与物块3连接的绳水平,与天花板连接的绳与水平方向成45°角,竖直绳悬挂重为20N的小球P.整个装置处于静止状态.则( )| A. | 物块1和2之间的摩擦力大小为0 | B. | 水平绳的拉力大小为15N | ||
| C. | 桌面对物块3的支持力大小为320N | D. | 物块3受5个力的作用 |
 如图所示,在一个直角三角形区域ABC内存在方向垂直于纸面向里、磁感应强度为B的匀强磁场,AB、BC、AC为磁场边界,AC边长为3l,∠A=53°.一质量为m、电荷量为+q的粒子从AB边上距A点为l的D点垂直于磁场边界AB射入匀强磁场.取sin53°=0.8,cos53°=0.6,求:
如图所示,在一个直角三角形区域ABC内存在方向垂直于纸面向里、磁感应强度为B的匀强磁场,AB、BC、AC为磁场边界,AC边长为3l,∠A=53°.一质量为m、电荷量为+q的粒子从AB边上距A点为l的D点垂直于磁场边界AB射入匀强磁场.取sin53°=0.8,cos53°=0.6,求: 图中左边有一对平行金属板,两板相距为d,电压为u,两板之间有匀强磁场,磁感应强度大小为B0,方向平行于板面并垂直于纸面朝里.图中右边有一边长为a的正三角形区域EFG( EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里,假设一系列质量不同、电荷量均为q的正离子沿平行于金属板面,垂直于磁场的方向射入金属板之间,均沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域.(不计重力)
图中左边有一对平行金属板,两板相距为d,电压为u,两板之间有匀强磁场,磁感应强度大小为B0,方向平行于板面并垂直于纸面朝里.图中右边有一边长为a的正三角形区域EFG( EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里,假设一系列质量不同、电荷量均为q的正离子沿平行于金属板面,垂直于磁场的方向射入金属板之间,均沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域.(不计重力)