题目内容
7.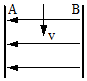 一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求:
一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求:(1)微粒进入电场后经过多少时间撞击到B板上.
(2)微粒竖直方向运动的距离.
分析 (1)粒子在平行金属板间做类平抛运动,水平方向匀加速运动,竖直方向匀速直线运动,根据牛顿第二定律求出加速度,由运动学公式求出时间;
(2)竖直方向匀速运动,由y=vt即可求出竖直方向运动的距离;
解答 解:(1)微粒在电场中类平抛运动,水平方向匀加速直线
根据牛顿第二定律:$q\frac{U}{d}=ma$
解得:$a=\frac{qU}{dm}$
水平位移:$\frac{d}{2}=\frac{1}{2}a{t}_{\;}^{2}$
$\frac{d}{2}=\frac{1}{2}\frac{qU}{dm}{t}_{\;}^{2}$
解得:$t=\sqrt{\frac{m{d}_{\;}^{2}}{qU}}$=$d\sqrt{\frac{m}{qU}}$
(2)竖直方向运动的距离$y=vt=vd\sqrt{\frac{m}{qU}}$
答:(1)微粒进入电场后经过时间$d\sqrt{\frac{m}{qU}}$撞击到B板上.
(2)微粒竖直方向运动的距离$vd\sqrt{\frac{m}{qU}}$
点评 该题考查了带电粒子在电场中偏转的问题,能熟练运用运动的合成与分解进行研究,掌握两个分运动的规律,根据类平抛运动的基本规律解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.关于电场线的说法正确的是( )
| A. | 电场线是为了形象的描述电场而假设的线 | |
| B. | 电场线就是电荷在电场中的运动轨迹 | |
| C. | 电场线是闭合的曲线 | |
| D. | 两条电场线在电场中可以相交 |
15. 平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
 平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )| A. | 微粒带负电 | B. | 动能逐渐增加 | ||
| C. | 电势能逐渐增加 | D. | 重力势能逐渐增加 |
2. 带电小球以速度v0沿竖直方向从A点垂直进入匀强电场E中,如图所示,经过一段时间后到达B点,其速度变为水平方向,大小仍为v0,则在上述过程中一定有( )
带电小球以速度v0沿竖直方向从A点垂直进入匀强电场E中,如图所示,经过一段时间后到达B点,其速度变为水平方向,大小仍为v0,则在上述过程中一定有( )
 带电小球以速度v0沿竖直方向从A点垂直进入匀强电场E中,如图所示,经过一段时间后到达B点,其速度变为水平方向,大小仍为v0,则在上述过程中一定有( )
带电小球以速度v0沿竖直方向从A点垂直进入匀强电场E中,如图所示,经过一段时间后到达B点,其速度变为水平方向,大小仍为v0,则在上述过程中一定有( )| A. | 小球一定不是做圆周运动 | |
| B. | 小球运动的水平位移大小等于竖直位移大小 | |
| C. | 静电力所做的功一定等于重力所做的功 | |
| D. | 小球速度的最小值为$\frac{v_0}{{\sqrt{2}}}$ |
12. 如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )
如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )
 如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )
如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )| A. | D点在N点的上方 | |
| B. | 运动到P点的速度为$\sqrt{2gR}$ | |
| C. | 从M到D的过程中,电势能先减小后增大 | |
| D. | 从P到D的过程中,动能减少量小于电势能增加量 |
16.对于闭合电路欧姆定律的理解,下列说法一定正确的是( )
| A. | 在电源电动势不变时,外电路的电阻越大,路端电压越大 | |
| B. | 在电源电动势不变时,外电路的电阻越大,电源内电压越大 | |
| C. | 当外电路断开时,路端电压的大小等于电源电动势 | |
| D. | 当外电路短路时,电源电动势为零 |
17.作加速直线运动的物体,当加速度逐渐减小时,在加速度减到零之前( )
| A. | 速度增大,位移减小 | B. | 速度减小,位移增大 | ||
| C. | 速度、位移都在增大 | D. | 速度、位移都在减小 |
 如图所示,电阻不计的两光滑金属导轨相距L固定在水平绝缘桌面上,其中半径为R的$\frac{1}{4}$圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端平齐.在与圆心等高的位置处有两金属棒MN、PQ垂直两导轨且与导轨接触良好.已知MN棒的质量为2m,电阻为r;PQ棒的质量为m,电阻也为r.开始时,保持PQ棒不动,将MN棒从圆弧导轨顶端无初速度释放,当MN棒脱离导轨后,再次由静止释放PQ棒,最后两棒都离开导轨落到地面上.MN、PQ两棒落地点到导轨边缘的水平距离之比为1:3.
如图所示,电阻不计的两光滑金属导轨相距L固定在水平绝缘桌面上,其中半径为R的$\frac{1}{4}$圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B、方向竖直向下的匀强磁场中,末端平齐.在与圆心等高的位置处有两金属棒MN、PQ垂直两导轨且与导轨接触良好.已知MN棒的质量为2m,电阻为r;PQ棒的质量为m,电阻也为r.开始时,保持PQ棒不动,将MN棒从圆弧导轨顶端无初速度释放,当MN棒脱离导轨后,再次由静止释放PQ棒,最后两棒都离开导轨落到地面上.MN、PQ两棒落地点到导轨边缘的水平距离之比为1:3. 如图所示,有一水平方向的匀强电场,场强大小为9000N/C,在电场内一水平面上作半径为10cm的圆,圆上取A、B两点,AO沿E方向,BO⊥OA,另在圆心处放一电量为10-8C的正点电荷,则A处场强大小EA为零.对(判断对错)
如图所示,有一水平方向的匀强电场,场强大小为9000N/C,在电场内一水平面上作半径为10cm的圆,圆上取A、B两点,AO沿E方向,BO⊥OA,另在圆心处放一电量为10-8C的正点电荷,则A处场强大小EA为零.对(判断对错)