题目内容
12. 如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )
如图所示,圆形槽光滑、绝缘、固定,圆心是O,最低点是P,半径为R,直径MN水平PQ竖直.a、b是两个完全相同的带正电小球(视为点电荷),质量为m,b固定在C点,C点为圆弧QN的中点,a从M点静止释放,沿半圆槽运动经过P点到达某点D(图中未画出)时速度为零.则小球a( )| A. | D点在N点的上方 | |
| B. | 运动到P点的速度为$\sqrt{2gR}$ | |
| C. | 从M到D的过程中,电势能先减小后增大 | |
| D. | 从P到D的过程中,动能减少量小于电势能增加量 |
分析 分析库仑力及重力的合力,根据功的公式明确合力做功情况;再根据重力做功和电场力做功的特点与势能的关系分析电势能的变化.
解答 解:A、带正电小球a如果到达N点上方,电场力和重力均做负功,D点速度不可能为0,所以D点在N点的下方,故A错误;
B、因为M、P到b球的距离相等,所以M、P在正电荷b的一个等势面上,所以从M到P电场力做功为0,根据动能定理:$mgR=\frac{1}{2}m{v}_{P}^{2}-0$,解得${v}_{P}^{\;}=\sqrt{2gR}$,故B正确;
C、从M到D的过程中,a、b两球距离先增加后减小,电场力先做正功后做负功,电势能先减小后增大,故C正确;
D、从P到D的过程中,动能减少,重力势能增加,电势能增加,所以动能减少量大于电势能增加量,故D错误;
故选:BC
点评 本题考查功能关系,要注意明确电场力和重力具有相同的性质,即重力做功量度重力势能的改变量;而电场力做功量度电势能的改变量.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
11.下列说法正确的是( )
| A. | 给电风扇供电时,电能全部转化为机械能 | |
| B. | 给电风扇供电时,电能主要转化为内能 | |
| C. | 给电热器供电时,电能几乎全部转化为内能 | |
| D. | 给电热器供电时,只有很少一部分电能转化为内能 |
3.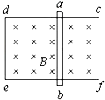 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )| A. | 金属棒中的感应电流的方向为b→a | |
| B. | 金属棒中的感应电流的大小为$\frac{{k{l^{\;}}}}{r}$ | |
| C. | 金属棒消耗的电功率为$\frac{{k}^{2}{l}^{4}}{r}$ | |
| D. | 若t=t1时金属棒仍然静止,金属棒受到的最大静摩擦力不能小于(B0+kt1)$\frac{{k{l^3}}}{r}$ |
20.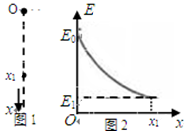 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )| A. | 从O到x1的过程中,小球的速率越来越大,加速度越来越大 | |
| B. | 电场强度大小恒定,方向沿x轴负方向 | |
| C. | 从O到x1的过程中,相等的位移内,小球克服电场力做的功相等 | |
| D. | 到达x1位置时,小球速度的大小为$\sqrt{\frac{2({E}_{1}-{E}_{0}+mg{x}_{1})}{m}}$ |
17.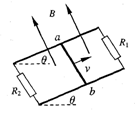 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
 如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )
如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为v时,受到安培力的大小为F.此时( )| A. | 整个装置因摩擦而消耗的热功率为μmgvcosθ | |
| B. | 整个装置消耗的机械功率为(F+μmgcosθ)v | |
| C. | 电阻R1消耗的热功率为$\frac{Fv}{3}$ | |
| D. | 电阻 R2消耗的热功率为 $\frac{Fv}{4}$ |
4.关于物理学研究方法的叙述中不正确的是( )
| A. | 根据平均速度的定义式,如果△t非常非常小,就可以认为$\frac{△x}{△t}$ 表示的是物体在t时刻的瞬时速度,在这里渗透了极限思想 | |
| B. | 在可以忽略物体的大小和形状时,能用质点来代替物体的方法叫综合分析法 | |
| C. | 把运动过程的“末态”作为“初态”的方向研究问题的方法称为逆向思维法 | |
| D. | 在推导匀变直线运动位移公式时,把整个运动过程等分成很多小段,每小段近似看做匀速直线运动,然后把各小段的位移相加,这里运用了微元分割法 |
1.在如图所示的电路中,当滑动变阻器R3的滑动触头P向下滑动时( )


| A. | 电压表示数变小 | B. | 电压表示数变大 | C. | 电流表示数变小 | D. | 电流表示数变大 |
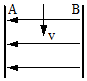 一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求:
一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求: