题目内容
19. 如图所示,有一水平方向的匀强电场,场强大小为9000N/C,在电场内一水平面上作半径为10cm的圆,圆上取A、B两点,AO沿E方向,BO⊥OA,另在圆心处放一电量为10-8C的正点电荷,则A处场强大小EA为零.对(判断对错)
如图所示,有一水平方向的匀强电场,场强大小为9000N/C,在电场内一水平面上作半径为10cm的圆,圆上取A、B两点,AO沿E方向,BO⊥OA,另在圆心处放一电量为10-8C的正点电荷,则A处场强大小EA为零.对(判断对错)
分析 根据公式E=k$\frac{Q}{{r}_{\;}^{2}}$求出点电荷在A点处产生的场强大小,判断出场强方向,A点的场强是由正点电荷和匀强电场场强的合成,根据平行四边形定则求解A点处的场强大小及方向.
解答 解:点电荷在A点的场强${E}_{点}^{\;}=k\frac{Q}{{r}_{\;}^{2}}=9×1{0}_{\;}^{9}×\frac{1{0}_{\;}^{-8}}{0.{1}_{\;}^{2}}N/C=9000N/C$
根据场强的叠加原理得,则两点的场强是由正点电荷和匀强电场场强的合成,A点的场强大小为
EA=E点-E匀=9×103N/C-9×103N/C=0,所以A处场强大小为0
故答案为:对
点评 本题电场的叠加问题,一要掌握点电荷的场强公式E=k$\frac{Q}{{r}_{\;}^{2}}$;二要能根据据平行四边形定则进行合成.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 某电场的电场强度E随时间t变化规律的图象如图6所示.当t=0时,在该电场中由静止释放一个带电粒子,设带电粒子只受电场力作用,则下列说法中正确的是( )
某电场的电场强度E随时间t变化规律的图象如图6所示.当t=0时,在该电场中由静止释放一个带电粒子,设带电粒子只受电场力作用,则下列说法中正确的是( )
 某电场的电场强度E随时间t变化规律的图象如图6所示.当t=0时,在该电场中由静止释放一个带电粒子,设带电粒子只受电场力作用,则下列说法中正确的是( )
某电场的电场强度E随时间t变化规律的图象如图6所示.当t=0时,在该电场中由静止释放一个带电粒子,设带电粒子只受电场力作用,则下列说法中正确的是( )| A. | 带电粒子将始终向同一个方向运动 | |
| B. | 带电粒子在0-3s内的初、末位置间的电势差为零 | |
| C. | 2s末带电粒子回到原出发点 | |
| D. | 0-2s内,电场力的总功不为零 |
4.关于物理学研究方法的叙述中不正确的是( )
| A. | 根据平均速度的定义式,如果△t非常非常小,就可以认为$\frac{△x}{△t}$ 表示的是物体在t时刻的瞬时速度,在这里渗透了极限思想 | |
| B. | 在可以忽略物体的大小和形状时,能用质点来代替物体的方法叫综合分析法 | |
| C. | 把运动过程的“末态”作为“初态”的方向研究问题的方法称为逆向思维法 | |
| D. | 在推导匀变直线运动位移公式时,把整个运动过程等分成很多小段,每小段近似看做匀速直线运动,然后把各小段的位移相加,这里运用了微元分割法 |
11.电源与外电阻R连接成闭合回路,对于电源的路端电压U,下列说法正确的是( )
| A. | 因U=IR,则U 与R的大小成正比 | |
| B. | 因U=IR,则R=0时,必有U=0 | |
| C. | 流过电源的电流越大,路端电压U也越大 | |
| D. | 若外电路断开,回路中电流为0,路端电压也等于0 |
8.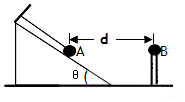 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则下列说法中正确的是( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则下列说法中正确的是( )
 如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则下列说法中正确的是( )
如图所示,水平地面上固定一个光滑绝缘斜面,斜面与水平面的夹角为θ.一根轻质绝缘细线的一端固定在斜面顶端,另一端系有一个带电小球A,细线与斜面平行.小球A的质量为m、电量为q.小球A的右侧固定放置带等量同种电荷的小球B,两球心的高度相同、间距为d.静电力常量为k,重力加速度为g,两带电小球可视为点电荷.小球A静止在斜面上,则下列说法中正确的是( )| A. | 小球A与B之间库仑力的大小为kq2/d | |
| B. | 当$\frac{q}{d}$=$\sqrt{\frac{mgsinθ}{k}}$时,细线上的拉力为0 | |
| C. | 当$\frac{q}{d}$=$\sqrt{\frac{mgtanθ}{k}}$时,细线上的拉力为0 | |
| D. | 当$\frac{q}{d}$=$\sqrt{\frac{mg}{ktanθ}}$时,斜面对小球A的支持力为0 |
9.关于自由落体运动,下列说法正确的是( )
| A. | 在空气中不考虑空气阻力的运动是自由落体运动 | |
| B. | 自由落体运动是初速度为零的匀加速直线运动 | |
| C. | 物体的质量越大,下落得越快 | |
| D. | 物体从静止开始下落的运动称为自由落体运动 |
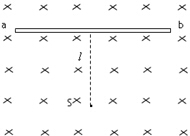 如图所示,磁场方向垂直于纸面向里,磁感应强度B=0.60T,磁场内有一块足够大平行感光板ab,板面与磁场方向平行,粒子发射源S向纸面内各个方向发射v=3.0×106m/s的正粒子,S到ab的距离l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求:
如图所示,磁场方向垂直于纸面向里,磁感应强度B=0.60T,磁场内有一块足够大平行感光板ab,板面与磁场方向平行,粒子发射源S向纸面内各个方向发射v=3.0×106m/s的正粒子,S到ab的距离l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求: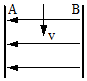 一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求:
一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求: