题目内容
15. 平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )
平行板电容器的两个极板与水平地面成30°角,两极板与一直流电源相连,上板接电源正极,若一带电微粒恰能沿图所示水平直线通过电容器,则在此过程中( )| A. | 微粒带负电 | B. | 动能逐渐增加 | ||
| C. | 电势能逐渐增加 | D. | 重力势能逐渐增加 |
分析 带电粒子在电场中受到电场力与重力,根据粒子的运动轨迹,结合运动的分析,可知电场力垂直极板向上,从而可确定粒子的运动性质,及根据电场力做功来确定电势能如何变化.
解答  解:A、根据题意可知,粒子做直线运动,则电场力与重力的合力与速度在同一直线上,所以电场力只能垂直极板向上,受力如图所示
解:A、根据题意可知,粒子做直线运动,则电场力与重力的合力与速度在同一直线上,所以电场力只能垂直极板向上,受力如图所示
因为上极板带正电,电场力方向与板间场强方向相反,故微粒带负电,故A正确;
B、根据受力图,粒子做直线运动,则电场力与重力的合力与速度方向反向,粒子做匀减速直线运动,动能逐渐减小,故B错误;
C、电场力与位移方向的夹角为钝角,所以电场力做负功,电势能逐渐增加,故C正确;
D、因为带电微粒沿水平直线运动,高度不变,重力势能不变,故D错误;
故选:AC
点评 考查根据运动情况来确定受力情况,并由电场力做功来确定电势能如何,以及动能的变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.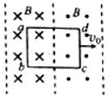 如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
 如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )
如图所示,三条直线之间的两个区域存在磁场,磁感应强度大小都为B,方向相反且垂直纸面.一宽为l的长方形闭合导线回路abcd,在纸面内以恒定速度v0向右运动,当运动到图示位置时( )| A. | 穿过回路磁通量的变化率为零 | |
| B. | 回路中感应电动势大小为Blv0 | |
| C. | 回路中感应电流的方向为a→b→c→d方向 | |
| D. | 回路中ab边与cd边所受安培力方向相同 |
3.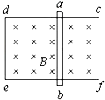 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )| A. | 金属棒中的感应电流的方向为b→a | |
| B. | 金属棒中的感应电流的大小为$\frac{{k{l^{\;}}}}{r}$ | |
| C. | 金属棒消耗的电功率为$\frac{{k}^{2}{l}^{4}}{r}$ | |
| D. | 若t=t1时金属棒仍然静止,金属棒受到的最大静摩擦力不能小于(B0+kt1)$\frac{{k{l^3}}}{r}$ |
20.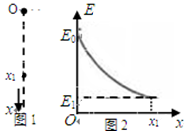 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
 某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )
某空间区域的竖直平面内存在电场,其中竖直的一条电场线如图1中虚线所示.一个质量为m、电荷量为q的带正电小球,在电场中从O点由静止开始沿电场线竖直向下运动.以O为坐标原点,取竖直向下为x轴的正方向,小球的机械能E与位移x的关系如图2所示,不计空气阻力.则( )| A. | 从O到x1的过程中,小球的速率越来越大,加速度越来越大 | |
| B. | 电场强度大小恒定,方向沿x轴负方向 | |
| C. | 从O到x1的过程中,相等的位移内,小球克服电场力做的功相等 | |
| D. | 到达x1位置时,小球速度的大小为$\sqrt{\frac{2({E}_{1}-{E}_{0}+mg{x}_{1})}{m}}$ |
4.关于物理学研究方法的叙述中不正确的是( )
| A. | 根据平均速度的定义式,如果△t非常非常小,就可以认为$\frac{△x}{△t}$ 表示的是物体在t时刻的瞬时速度,在这里渗透了极限思想 | |
| B. | 在可以忽略物体的大小和形状时,能用质点来代替物体的方法叫综合分析法 | |
| C. | 把运动过程的“末态”作为“初态”的方向研究问题的方法称为逆向思维法 | |
| D. | 在推导匀变直线运动位移公式时,把整个运动过程等分成很多小段,每小段近似看做匀速直线运动,然后把各小段的位移相加,这里运用了微元分割法 |
5.空间某一静电场方向平行于x轴,电势φ随x变化情况如图所示,下列说法中正确的是( )


| A. | 电场场强的方向始终指向x轴的正方向 | |
| B. | x1处的电场场强小于x2处的电场场强 | |
| C. | 正电荷沿x轴从O移到x1的过程中,电场力先做负功,后做正功 | |
| D. | 负电荷沿x轴从O移到无限远处的过程中,电场力先做负功,后做正功 |
 用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.
用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.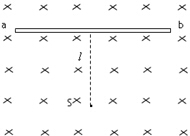 如图所示,磁场方向垂直于纸面向里,磁感应强度B=0.60T,磁场内有一块足够大平行感光板ab,板面与磁场方向平行,粒子发射源S向纸面内各个方向发射v=3.0×106m/s的正粒子,S到ab的距离l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求:
如图所示,磁场方向垂直于纸面向里,磁感应强度B=0.60T,磁场内有一块足够大平行感光板ab,板面与磁场方向平行,粒子发射源S向纸面内各个方向发射v=3.0×106m/s的正粒子,S到ab的距离l=16cm.已知粒子的比荷$\frac{q}{m}$=5.0×107C/kg,求: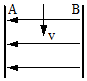 一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求:
一微粒以速度v竖直向下从正中间射入水平方向的匀强电场,如图所示.如果A、B两板间距离为d,电势差为U.微粒质量为m,电量为q,不计重力影响,两金属板足够长.求: