题目内容
13. 质量可忽略的杆,长L=0.5m,一端连有质量m=2kg的小球,它们在竖直平面内绕O点做圆周运动.如图所示,求下列情况下,球通过最高点时,杆受到的球所施加的作用力(计算出大小,并说明是拉力还是压力,g取10m/s2):
质量可忽略的杆,长L=0.5m,一端连有质量m=2kg的小球,它们在竖直平面内绕O点做圆周运动.如图所示,求下列情况下,球通过最高点时,杆受到的球所施加的作用力(计算出大小,并说明是拉力还是压力,g取10m/s2):(1)当v=1m/s时,杆受到的力多大,是什么力?
(2)当v=4m/s时,杆受到的力多大,是什么力?
分析 球通过最高点时,由重力和杆对小球的作用力的合力提供向心力,以小球为研究对象,根据牛顿第二定律求解.
解答 解:(1)当杆恰好不受力时,重力提供向心力,根据牛顿第二定律得:
$\frac{m{v}_{0}^{2}}{L}=mg$
故v0=2m/s
当v=1m/s时<v0,杆对小球的作用力的方向向上,则:
$mg-{F}_{1}=\frac{m{v}_{1}^{2}}{L}$
代入数据得:F1=16N
根据牛顿第三定律,杆受到向下的16N的压力.
(2)当小球以速度v=4m/s通过最高点时,有:${F}_{2}+mg=\frac{m{v}_{2}^{2}}{L}$
故F2=44N,方向竖直向上.
根据牛顿第三定律可知,杆受到的力的方向向上,大小是44N
答:(1)当小球以1m/s速度通过最高点时,杆受到向下的16N的压力;
(2)当小球以速度v=4m/s通过最高点时,球对杆的作用力是拉力,大小是44N,方向是竖直向上.
点评 解决本题的关键知道“杆模型”中拉力与支持力的临界速度,分析物体受力,确定向心力的来源,再运用牛顿第二定律求解.

练习册系列答案
相关题目
3. 直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )
直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )
 直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )
直角三角形金属框abc放置在竖直向上的匀强磁场中,磁感应强度大小为B,方向平行于ab边向上,若金属框绕ab边向纸面外以角速度ω匀速转动90°(从上往下看逆时针转动),如图甲所示,c、a两点的电势差为Uca,通过ab边的电荷量为q,若金属框绕bc边向纸面内以角速度ω匀速转动90°,如图乙所示,c、a两点的电势差为Uca′,通过ab边的电荷量为q′,已知bc、ab边的长度都为l,金属框的总电阻为R,下列判断正确的是( )| A. | Uca=$\frac{1}{2}$Bωl2 | B. | Uca′=$\frac{1}{2}$Bωl2 | C. | q=$\frac{\sqrt{2}Bπ{l}^{2}}{8R}$ | D. | q′=$\frac{B{l}^{2}}{2R}$ |
8. 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$;sin$\frac{4}{5}$,cos53°=$\frac{3}{5}$)( )
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$;sin$\frac{4}{5}$,cos53°=$\frac{3}{5}$)( )
 如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$;sin$\frac{4}{5}$,cos53°=$\frac{3}{5}$)( )
如图所示,有一固定的且内壁光滑的半球面,球心为O,最低点为C,在其内壁上有两个质量相同的小球(可视为质点)A和B,在两个高度不同的水平面内做匀速圆周运动,A球的轨迹平面高于B球的轨迹平面,A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°,以最低点C所在的水平面为重力势能的参考平面,则(sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$;sin$\frac{4}{5}$,cos53°=$\frac{3}{5}$)( )| A. | A、B两球所受支持力的大小之比为4:3 | |
| B. | A、B两球运动的周期之比为4:3 | |
| C. | A、B两球的线速度之比为8:5 | |
| D. | A、B两球的角速度之比为1:1 |
18.关于黑体与黑体辐射,下列说法错误的是( )
| A. | 一般物体辐射电磁波的情况与温度无关,只与材料的种类及表面情况有关 | |
| B. | 黑体能完全吸收入射的各种波长的电磁波而不发生反射 | |
| C. | 带电微粒辐射和吸收的能量,只能是某一最小能量值的整数倍 | |
| D. | 黑体辐射随着温度的升高,各种波长的辐射强度都增加且辐射强度的极大值向波长较短的方向移动 |
2.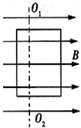 (多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )
(多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )
 (多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )
(多选)在匀强磁场中匀速转动的矩形线圈的周期为T,转轴01O2垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么( )| A. | 线圈中感应电流的有效值为2A | |
| B. | 线圈消耗的电功率为4W | |
| C. | 任意时刻线圈中的感应电动势为e=4cos$\frac{2π}{T}$t | |
| D. | 任意时刻穿过线圈的磁通量为Φ=$\frac{T}{π}$sin$\frac{2π}{T}$t |
3.卡车在平直公路上从静止开始加速行驶,经时间t前进距离l,速度达到最大值vm,设此过程中发动机功率恒为P,卡车所受阻力为f,则这段时间内,发动机所做的功为( )
| A. | Pt-fl | B. | fl | C. | Pt | D. | Pt+fl |