题目内容
5.已知氢原子处于基态时的能量为E1(E1<0),氢原子处于n能级时能量为En=$\frac{{E}_{1}}{{n}^{2}}$,现有一个处于n=3能级的氢原子向低能级跃迁,其恰好可以发出两个不同频率的光子,用其中频率较小的光子照射某种金属恰能使该金属发生光电效应,已知普朗克常量为h.(1)求该金属发生光电效应的截止频率;
(2)若用其中频率较大的光子照射该金属,求产生的光电子的最大初动能?
分析 (1)抓住跃迁中频率较小的光子恰好使某种金属发生光电效应,结合能级差求出逸出功,根据逸出功和截止频率的关系求出金属发生光电效应的截止频率.
(2)根据能级差求出频率较大光子的能量,结合光电效应方程求出产生的光电子最大初动能.
解答 解:(1)氢原子处于n能级时能量为En=$\frac{{E}_{1}}{{n}^{2}}$,则有:${E}_{2}=\frac{{E}_{1}}{4}$,${E}_{3}=\frac{{E}_{1}}{9}$,
恰好发生光电效应,逸出功为:$W=h{v}_{0}={E}_{3}-{E}_{2}=-\frac{5{E}_{1}}{36}$,
解得极限频率为:${v}_{0}=\frac{W}{h}=-\frac{5{E}_{1}}{36h}$.
(2)能量较大的光子为:$hv={E}_{2}-{E}_{1}=-\frac{3{E}_{1}}{4}$,
根据光电效应方程Ekm=hv-W得:${E}_{km}=-\frac{11}{18}{E}_{1}$.
答:(1)该金属发生光电效应的截止频率为$-\frac{5{E}_{1}}{36h}$;
(2)产生的光电子的最大初动能为$-\frac{11}{18}{E}_{1}$.
点评 解决本题的关键知道释放光子的能量与能级差之间的关系,掌握光电效应方程,并能灵活运用.

练习册系列答案
相关题目
15.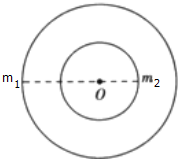 某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )
某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )
 某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )
某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )| A. | 它们的角速度相同 | B. | 它们的线速度相同 | ||
| C. | m1>m2 | D. | 它们的加速度相同 |
16.一个按正弦规律变化的交变电流的i-t图象如图所示.根据图象可以断定( )


| A. | 交变电流的频率 f=0.2 Hz | |
| B. | 交变电流的有效值I=20$\sqrt{2}$A | |
| C. | 交变电流瞬时值表达式 i=20sin0.02t A | |
| D. | 在t=$\frac{T}{8}$时刻,电流的大小与其有效值相等 |
20.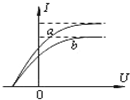 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | 两种光在光电管内的波长关系为λa>λb | |
| B. | 照射该光电管时a光使其逸出的光电子最大初动能大 | |
| C. | 实验中a的光的强度大于b光 | |
| D. | a光光子能量大于b光光子能量 |
10. 如图所示,顶端附有光滑定滑轮的斜面体静止在粗糙水平面上,三条细绳结于O点.一条绳跨过定滑轮平行于斜面连接物块P,一条绳连接小球Q,P、Q两物体处于静止状态,另一条绳OA在外力F的作用下使夹角θ<90°,现缓慢改变绳OA的方向至θ>90°,且保持结点O位置不变,整个装置始终处于静止状态.下列说法正确的是( )
如图所示,顶端附有光滑定滑轮的斜面体静止在粗糙水平面上,三条细绳结于O点.一条绳跨过定滑轮平行于斜面连接物块P,一条绳连接小球Q,P、Q两物体处于静止状态,另一条绳OA在外力F的作用下使夹角θ<90°,现缓慢改变绳OA的方向至θ>90°,且保持结点O位置不变,整个装置始终处于静止状态.下列说法正确的是( )
 如图所示,顶端附有光滑定滑轮的斜面体静止在粗糙水平面上,三条细绳结于O点.一条绳跨过定滑轮平行于斜面连接物块P,一条绳连接小球Q,P、Q两物体处于静止状态,另一条绳OA在外力F的作用下使夹角θ<90°,现缓慢改变绳OA的方向至θ>90°,且保持结点O位置不变,整个装置始终处于静止状态.下列说法正确的是( )
如图所示,顶端附有光滑定滑轮的斜面体静止在粗糙水平面上,三条细绳结于O点.一条绳跨过定滑轮平行于斜面连接物块P,一条绳连接小球Q,P、Q两物体处于静止状态,另一条绳OA在外力F的作用下使夹角θ<90°,现缓慢改变绳OA的方向至θ>90°,且保持结点O位置不变,整个装置始终处于静止状态.下列说法正确的是( )| A. | 绳OA的拉力先减小后增大 | |
| B. | 斜面对物块P的摩擦力的大小可能先减小后增大 | |
| C. | 地面对斜面体有向右的摩擦力 | |
| D. | 地面对斜面体的支持力等于物块P和斜面体的重力之和 |
17. 如图所示,固定在地面上、截面圆心为O、半径为R、表面粗糙的半圆柱体,其上方固定一个光滑曲线轨道AB,AB间的竖直高度为R,轨道底端水平并与半圆柱体顶端相切于B点.质量为m的小球从A点沿轨道AB由静止开始滑下,最后在水平面上的落点为C(图中未画出),则下列说法正确的是( )
如图所示,固定在地面上、截面圆心为O、半径为R、表面粗糙的半圆柱体,其上方固定一个光滑曲线轨道AB,AB间的竖直高度为R,轨道底端水平并与半圆柱体顶端相切于B点.质量为m的小球从A点沿轨道AB由静止开始滑下,最后在水平面上的落点为C(图中未画出),则下列说法正确的是( )
 如图所示,固定在地面上、截面圆心为O、半径为R、表面粗糙的半圆柱体,其上方固定一个光滑曲线轨道AB,AB间的竖直高度为R,轨道底端水平并与半圆柱体顶端相切于B点.质量为m的小球从A点沿轨道AB由静止开始滑下,最后在水平面上的落点为C(图中未画出),则下列说法正确的是( )
如图所示,固定在地面上、截面圆心为O、半径为R、表面粗糙的半圆柱体,其上方固定一个光滑曲线轨道AB,AB间的竖直高度为R,轨道底端水平并与半圆柱体顶端相切于B点.质量为m的小球从A点沿轨道AB由静止开始滑下,最后在水平面上的落点为C(图中未画出),则下列说法正确的是( )| A. | 小球将沿圆柱体表面做圆周运动滑至C点 | |
| B. | 小球将沿圆柱体表面运动一段后脱离表面斜下抛至C点 | |
| C. | 小球将做平抛运动到达C点 | |
| D. | O、C之间的距离为2R |
14.电荷周围存在着一种特殊的物质叫做( )
| A. | 元电荷 | B. | 电场 | C. | 电荷量 | D. | 磁场 |
 质量可忽略的杆,长L=0.5m,一端连有质量m=2kg的小球,它们在竖直平面内绕O点做圆周运动.如图所示,求下列情况下,球通过最高点时,杆受到的球所施加的作用力(计算出大小,并说明是拉力还是压力,g取10m/s2):
质量可忽略的杆,长L=0.5m,一端连有质量m=2kg的小球,它们在竖直平面内绕O点做圆周运动.如图所示,求下列情况下,球通过最高点时,杆受到的球所施加的作用力(计算出大小,并说明是拉力还是压力,g取10m/s2):