题目内容
14.科学家在地球轨道外侧发现了一颗绕太阳运行的小行星,小行星的公转轨道与地球的公转轨道平面重合且运行方向相同,经过观察,该小行星相邻两次与地球相距最近的时间间隔为t,已知地球绕太阳公转半径为R,周期为T,设地球的公转轨道和小行星的公转轨道都是圆轨道,不考虑地球与小行星之间的作用力,求小行星与地球的最近距离.分析 该小行星每隔t时间与地球相遇一次,根据△ω•t=2π列式求解小行星周期;小行星与地球的最近距离等于两者的轨道半径之差.
解答 解:设小行星运行周期为T1,根据题意,有:
$\frac{2π}{T}$t-$\frac{2π}{{T}_{1}}$t=2π;
对地球:
$\frac{Gmm}{{R}^{2}}$=m($\frac{2π}{T}$)2R;
对小行星:
$\frac{GM{m}_{1}}{{R}_{1}^{2}}$=m1($\frac{2π}{{T}_{1}}$)2R1;
故R1=$\root{3}{\frac{{t}^{2}}{(t-T)^{2}}}$R;
故小行星与地球最近距离S=R1-R=($\root{3}{\frac{{t}^{2}}{{(t-T)}^{2}}}$-1)R;
答:小行星与地球的最近距离为($\root{3}{\frac{{t}^{2}}{{(t-T)}^{2}}}$-1)R.
点评 本题关键根据相对运动知识求解出小行星的周期,然后根据万有引力提供向心力列式求解,不难.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.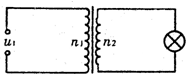 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )| A. | Um=200V | B. | Um=200$\sqrt{2}V$ | ||
| C. | 当ωt=$\frac{π}{2}$时,副线圈中的电流为O | D. | 当ωt=π时,副线圈中的电流为O |
9.材料一:2010年7月21日,中国首座快中子反应堆达到临界,它的最大特点是可以再次利用燃料产生的“核垃圾”使铀资源的利用率大幅度提高.当铀238俘获中子以后,经过两次β衰变为钚239,钚239衰变为铀235.
材料二:欧洲核子研究中心的科学家们在2010年11月17日表示,通过大型强子对撞机俘获了少量的“反氢原子”.其核内有一个带有负电的质子,核外有一个带正电的电子.反氢原子与氢原子互称为反物质,相遇时发生湮灭,并释放出大量能量,不产生剩余核辐射.
根据以上信息判断下列说法正确的是( )
材料二:欧洲核子研究中心的科学家们在2010年11月17日表示,通过大型强子对撞机俘获了少量的“反氢原子”.其核内有一个带有负电的质子,核外有一个带正电的电子.反氢原子与氢原子互称为反物质,相遇时发生湮灭,并释放出大量能量,不产生剩余核辐射.
根据以上信息判断下列说法正确的是( )
| A. | 铀238俘获中子的核反应方程是92238U+01n→94239Pu+2-10e | |
| B. | 钚239衰变为铀235的核反应方程是94239Pu→92235U+24He | |
| C. | 反氢原子高速撞击氢原子发生湮灭,该反应不遵循动量守恒定律 | |
| D. | 质量均为m的氢原子与反氢原子相遇时发生湮灭,释放的能量为E=mc2 |
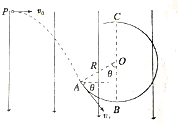 如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求:
如图所示,在环球地球做匀速圆周运动的人造地球卫星内部,光滑绝缘圆弧轨道ABC在竖直平面内,圆弧的半径R=0.3m.整个区域处在方向竖直向下的匀强电场中,一个质量为m=0.6kg带正电,电量为q的小球(qE=mg)以初速度v0=2m/s从P点水平抛出,恰好从A点的切线方向进入圆弧轨道,已知θ=60°,小球后来继续沿轨道运动经过C点.(进入圆弧时无机械能损失,取g=10m/s2)求: 如图所示,高一年级某同学正在进行“引体向上”项目的测试,该同学在这次测试中一分钟完成了20个“引体向上”,若他每次“引体向上”中心上升约0.5m,则该同学在本次测试中做功的平均功率最接近( )
如图所示,高一年级某同学正在进行“引体向上”项目的测试,该同学在这次测试中一分钟完成了20个“引体向上”,若他每次“引体向上”中心上升约0.5m,则该同学在本次测试中做功的平均功率最接近( )