题目内容
16.在“探究弹力与弹簧伸长量的关系”时,某同学把两根轻弹簧按如图1所示连接起来进行探究.
(1)某次测量结果如图2所示,指针示数为16.00cm.
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如表格所示.用表中数据计算弹簧Ⅰ的劲度系数为12.5N/m,弹簧Ⅱ的劲度系数为27.8N/m(取g=10m/s2,结果均保留三位有效数字).
| 钩码数 | 1 | 2 | 3 | 4 |
| LA/cm | 15.71 | 19.71 | 23.70 | 27.70 |
| LB/cm | 29.96 | 35.76 | 41.55 | 47.34 |
分析 (1)刻度尺的读数需读到最小刻度的下一位.
(2)根据弹簧Ⅰ形变量的变化量,结合胡克定律求出劲度系数.通过弹簧Ⅱ弹力的变化量和形变量的变化量可以求出弹簧Ⅱ的劲度系数.
解答 解:(1)指针示数为16.00cm.
(2)表格中的数据可知,当弹力的变化量△F=0.5N时,弹簧形变量的变化量为△x=4.00cm,根据胡克定律知:
${k}_{1}=\frac{△F}{△x}=\frac{0.5}{0.04}$N/m=12.5N/m.
结合A、B示数的变化,可得当弹力的变化量△F=0.5N时,弹簧Ⅱ形变量的变化量△x=5.80-4.00=1.80cm,根据胡克定律能求出弹簧Ⅱ的劲度系数k2=$\frac{△F}{△x}$=$\frac{0.5}{0.018}$N/m=27.8N/m.
故答案为:(1)16.00 (2)12.5 27.8
点评 解决本题的关键掌握胡克定律,知道F=kx,x表示形变量,以及知道其变形式△F=k△x,△x为形变量的变化量

练习册系列答案
相关题目
7.某一物体在质量不变的情况下,下列说法中正确的是( )
| A. | 物体动量改变,其速度大小一定改变 | |
| B. | 物体的速度方向改变,其动量不一定改变 | |
| C. | 物体做平抛运动时,在任意相等的时间内动量的变化量相同 | |
| D. | 物体的动能不变,其动量可能改变 |
4.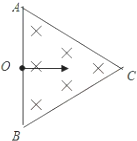 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | ||
| C. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
11. 如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
 如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )
如图所示,A、B是等量异种电荷连线上的两点,ABCD是关于两电荷连线的垂直平分线对称的矩形,则关于A、B、C、D各点的电场强度大小EA、BB、EC、ED及各点的电势φA、φB、φC、φD的说法正确的是( )| A. | φA>φD>φC>φB | B. | EA>BD>EC>EB | C. | φA=φB>φC=φD | D. | EA=BB<EC=ED |
6. 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )| A. | φ1<φ2<φ3<φ4 | |
| B. | 粒子的运动轨迹和φ3等势面也可能垂直 | |
| C. | φ4等势面上各点场强处处相等 | |
| D. | 该区域可能是点电荷和无限大金属平板形成的电场 |
 做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2).
做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2). 如图所示为圆形轨道的四分之三,圆轨道半径为0.5m,把它固定在水平地面在轨道最底端放置两个小球,A球质量为0.2kg,B球质量为0.4kg,中间有塑胶炸药,现把塑胶炸药引爆,两小球被推开,已知A球刚好能通过圆的最高点.(g=10m/s2)求:
如图所示为圆形轨道的四分之三,圆轨道半径为0.5m,把它固定在水平地面在轨道最底端放置两个小球,A球质量为0.2kg,B球质量为0.4kg,中间有塑胶炸药,现把塑胶炸药引爆,两小球被推开,已知A球刚好能通过圆的最高点.(g=10m/s2)求: 如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,则
如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,则