题目内容
6. 做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2).
做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2).
分析 平抛运动在竖直方向上做自由落体运动,在水平方向做匀速直线运动,根据竖直向上△h=gT2,求出相等的时间间隔,再根据水平方向的水平位移,求出平抛运动的初速度.
根据某段时间内的平均速度等于中间时刻的瞬时速度求出第二个图在竖直方向上的分速度,结合速度时间公式求出落地的速度,根据速度位移公式求出平台离地的高度.
解答 解:在竖直方向上,根据△y=gT2得,T=$\sqrt{\frac{△y}{g}}=\sqrt{\frac{L}{g}}=\sqrt{\frac{3.6}{10}}s=0.6s$,
则汽车离开平台的速度${v}_{0}=\frac{x}{T}=\frac{3.6×2}{0.6}m/s=12m/s$.
第二个图竖直方向上的瞬时速度${v}_{y2}=\frac{3×3.6}{2×0.6}=9m/s$,
则落地的竖直分速度vy=vy2+gT=9+10×0.6m/s=15m/s,
高台离地面的高度h=$\frac{{{v}_{y}}^{2}}{2g}=\frac{225}{20}m=11.25m$.
故答案为:12,11.25.
点评 解决本题的关键知道平抛运动在竖直方向上做自由落体运动,在水平方向做匀速直线运动,且分运动和合运动具有等时性,结合运动学公式和推论灵活求解.

练习册系列答案
相关题目
1.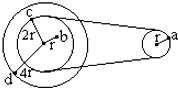 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )| A. | a点与b点的线速度大小相等 | |
| B. | a点与b点的角速度大小相等 | |
| C. | a点与c点的线速度大小相等 | |
| D. | a点的向心加速度小于d点的向心加速度 |
11.发现行星运动规律并分别于1609年和1619年发表了行星运动三定律的物理学家是( )
| A. | 伽利略 | B. | 开普勒 | C. | 第谷 | D. | 欧姆 |
16.在“探究弹力与弹簧伸长量的关系”时,某同学把两根轻弹簧按如图1所示连接起来进行探究.
(1)某次测量结果如图2所示,指针示数为16.00cm.
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如表格所示.用表中数据计算弹簧Ⅰ的劲度系数为12.5N/m,弹簧Ⅱ的劲度系数为27.8N/m(取g=10m/s2,结果均保留三位有效数字).

(1)某次测量结果如图2所示,指针示数为16.00cm.
(2)在弹性限度内,将50g的钩码逐个挂在弹簧下端,得到指针A、B的示数LA和LB如表格所示.用表中数据计算弹簧Ⅰ的劲度系数为12.5N/m,弹簧Ⅱ的劲度系数为27.8N/m(取g=10m/s2,结果均保留三位有效数字).
| 钩码数 | 1 | 2 | 3 | 4 |
| LA/cm | 15.71 | 19.71 | 23.70 | 27.70 |
| LB/cm | 29.96 | 35.76 | 41.55 | 47.34 |

 在“验证机械能守恒定律”的实验中,所用电源的频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.若按实验要求正确地选出纸带进行测量,量得连续三点A、B、C到第一个点的距离如图所示(相邻计数点时间间隔为0.02s),那么:
在“验证机械能守恒定律”的实验中,所用电源的频率为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.若按实验要求正确地选出纸带进行测量,量得连续三点A、B、C到第一个点的距离如图所示(相邻计数点时间间隔为0.02s),那么: 如图所示,斜面ABC中AB段l1=2m且光滑,BC段l2=1m且粗糙,质量为1kg的小物块由A点以一定的初速度沿斜面向上滑行,到达B点速度vB=4m/s,到达C点速度为零,此过程中小物块在BC段速度的变化率是AB段的2倍,g=10m/s2,求:
如图所示,斜面ABC中AB段l1=2m且光滑,BC段l2=1m且粗糙,质量为1kg的小物块由A点以一定的初速度沿斜面向上滑行,到达B点速度vB=4m/s,到达C点速度为零,此过程中小物块在BC段速度的变化率是AB段的2倍,g=10m/s2,求: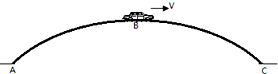 如图所示,是公路上的拱形桥,B是拱形桥的最高点,桥面的圆弧ABC所在圆的半径为R=400m. 现有一质量为m=2×103kg的汽车以恒定的功率P=3×106w过桥.在过最高点B时,汽车受牵引力F=3×105N.取g=10N/kg,小车视为质点,求:
如图所示,是公路上的拱形桥,B是拱形桥的最高点,桥面的圆弧ABC所在圆的半径为R=400m. 现有一质量为m=2×103kg的汽车以恒定的功率P=3×106w过桥.在过最高点B时,汽车受牵引力F=3×105N.取g=10N/kg,小车视为质点,求: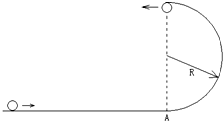 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出: