题目内容
13. 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )| A. | 卫星甲的周期最大 | |
| B. | 卫星甲、乙经过P点时的加速度大小相等 | |
| C. | 三个卫星在远地点的速度可能大于第一宇宙速度 | |
| D. | 如果地球自转的角速度突然变为原来的$\frac{(g+a)}{a}$倍,那么赤道上的物体将会“飘”起来 |
分析 根据开普勒第三定律知,椭圆半长轴越大,卫星的周期越大.由牛顿第二定律研究加速度,使地球上的物体票“飘”起来即物体处于完全失重状态,即此时物体所受地球的重力完全提供物体随地球自转时的向心力.
解答 解:A、根据开普勒第三定律知,椭圆半长轴越大,卫星的周期越大,卫星甲的半长轴最大,故甲的周期最大,故A正确;
B、根据牛顿第二定律得:$G\frac{Mm}{{r}^{2}}=ma$,得卫星的加速度a=$G\frac{M}{{r}^{2}}$,M是地球的质量,r是卫星到地心的距离,卫星甲、乙分别经过P点时r相同,则加速度相等,故B正确;
C、根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得$v=\sqrt{\frac{GM}{r}}$,轨道半径越小,速度越大,当轨道半径最小等于地球半径时,速度等于第一宇宙速度.
假设一位卫星绕经过远地点的圆轨道做圆周运动,则此卫星的速度一定小于第一宇宙速度,卫星从该轨道进入椭圆轨道,要做减速运动,速度要变小,故三个卫星的速度均小于第一宇宙速度,故C错误;
D、使地球上的物体票“飘”起来即物体处于完全失重状态,即此时物体所受地球的重力完全提供物体随地球自转时的向心力则有:$G\frac{Mm}{{R}^{2}}-mg=ma$,当物体飘起来的时候,万有引力完全提供向心力,则$G\frac{Mm}{{R}^{2}}=m(g+a)$,即此时的向心加速度a′=g+a
根据向心加速度和角速度的关系有:a=Rω2,a′=Rω′2可得:$ω′=\sqrt{\frac{g+a}{a}}ω$,故D错误.
故选:AB
点评 卫星绕地球运动,轨道高度越大,发射速度越大,发射越困难,卫星在近地点的速度越大.在随圆轨道上运动的卫星,万有引力和卫星运动所需要向心力不是始终相等的,故在椭圆轨道上运动的卫星不是始终处于完全失重状态.

| A. | 量子卫星的轨道平面可能与北京同纬度的轨道平面重合 | |
| B. | 量子卫星运行的周期比同步卫星的运行周期大 | |
| C. | 量子卫星运行的线速度比同步卫星运行的线速度小 | |
| D. | 量子卫星运行的向心加速度比同步卫星运行的向心加速度大 |
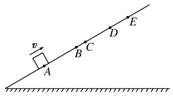 如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )
如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )| A. | 通过A点的速率为8 m/s | B. | 通过B点的速率为$\sqrt{10}$ m/s | ||
| C. | 通过C点的速率为6 m/s | D. | CD:DE=5:4 |

| A. | A点的场强大 | B. | B点的场强大 | ||
| C. | B点的电势高 | D. | 正电荷在B点的电势能高 |
 如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上侧与大气相通,下端开口处开关K关闭,A侧空气柱的长度为l=10.0cm,B侧水银面比A侧的高h=3.0cm,现将开关K打开,从U形管中放出部分水银,当两侧的高度差为h1=10.0cm时,将开关K关闭,已知大气压强P0=75.0cmHg.
如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上侧与大气相通,下端开口处开关K关闭,A侧空气柱的长度为l=10.0cm,B侧水银面比A侧的高h=3.0cm,现将开关K打开,从U形管中放出部分水银,当两侧的高度差为h1=10.0cm时,将开关K关闭,已知大气压强P0=75.0cmHg.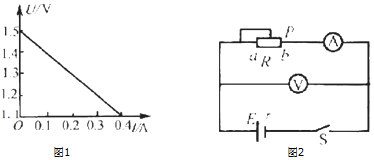
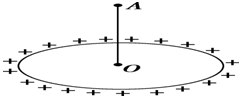 如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.
如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.