题目内容
3.两个行星的质量分别为m和3m,绕太阳运动的轨道半径分别为2r和3r,求:(1)它们与太阳间的引力之比;
(2)它们的公转周期之比.
分析 (1)根据万有引力定律即可求出它们与太阳间的引力之比.
(2)根据G$\frac{M{m}_{\;}}{{r}^{2}}$=$\frac{4{π}^{2}m}{{T}^{2}}r$解答.
解答 解:(1)设太阳的质量为M,根据F=G$\frac{M{m}_{\;}}{{r}^{2}}$,知它们的引力之比为:$\frac{GM{m}_{1}}{{{R}^{2}}_{1}}$:$\frac{GM{m}_{2}}{{R}_{2}^{2}}$=$\frac{{m}_{1}}{{m}_{2}}:\frac{{R}_{1}^{2}}{{R}_{2}^{2}}$=$\frac{1}{3}$:($\frac{2r}{3r}$)2=3:4
(2)根据F=G$\frac{M{m}_{\;}}{{r}^{2}}$=$\frac{4{π}^{2}m}{{T}^{2}}r$知T=2$π\sqrt{\frac{{r}^{3}}{GM}}$,知它们的周期之比为:2$π\sqrt{\frac{{R}_{1}^{3}}{GM}}$:2$π\sqrt{\frac{{R}_{2}^{3}}{GM}}$=$\sqrt{(2r)^{3}}:\sqrt{(3r)^{3}}$=$\sqrt{8}$:$\sqrt{27}$
答:(1)它们与太阳间的引力之比是3:4;
(2)它们的公转周期之比是$\sqrt{8}$:$\sqrt{27}$.
点评 本题考查万有引力定律的应用,属于简单题目,注意根据公式变出所要求的物理量的表达式,再进行比例求解.

练习册系列答案
相关题目
13. 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )| A. | 卫星甲的周期最大 | |
| B. | 卫星甲、乙经过P点时的加速度大小相等 | |
| C. | 三个卫星在远地点的速度可能大于第一宇宙速度 | |
| D. | 如果地球自转的角速度突然变为原来的$\frac{(g+a)}{a}$倍,那么赤道上的物体将会“飘”起来 |
14.据报道,美国国家航空航天局宣布首次在太阳系外发现“类地”行星,假如宇航员乘坐宇宙飞船到达该行星,进行科学观测,得到该行星的自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放一个小球(引力视为恒力),落地时间为t.已知该行星半径为R,万有引力常量为G,则下列说法正确的是( )
| A. | 该行星的第一宇宙速度为$\frac{πR}{T}$ | |
| B. | 宇宙飞船绕该星球做圆周运动的周期不小于πt$\sqrt{\frac{2R}{h}}$ | |
| C. | 该行星的平均密度为$\frac{3π}{{T}^{2}G}$ | |
| D. | 如果该行星存在一颗同步卫星,其距行星表面高度为$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$-R |
18.一些星球由于某种原因而发生收缩,假设该星球的直径缩小到原来一半的.若收缩时质量不变,不考虑星球自转的影响,则与收缩前相比( )
| A. | 同一物体在星球表面受到的重力增大到原来的4倍 | |
| B. | 同一物体在星球表面受到的重力增大到原来的16倍 | |
| C. | 该星球的平均密度增大到原来的8倍 | |
| D. | 该星球的平均密度增大到原来的64倍 |
8.质点是一个理想化的物理模型,下列关于把物体或人看做质点的说法正确的是( )
| A. | 体积很小的物体,一定能被看做质点 | |
| B. | 圆形物体都可以被看做质点,长方形物体都不能被看做质点 | |
| C. | 人在进行马拉松比赛时,确定其在比赛中的位置时可把人看做质点 | |
| D. | 只有以地面为参考系时,物体才能被看做质点 |
15. 如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1s,2s,2.5s,3s.下列说法正确的是( )
如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1s,2s,2.5s,3s.下列说法正确的是( )
 如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1s,2s,2.5s,3s.下列说法正确的是( )
如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1s,2s,2.5s,3s.下列说法正确的是( )| A. | 物体在AB段的平均速度大小为1 m/s | |
| B. | 物体在ABC段的平均速度大小为$\frac{\sqrt{5}}{2}$m/s | |
| C. | AB段的平均速度比ABC段的平均速度更能反映物体处于A点时的瞬时速度 | |
| D. | 物体在AB段的平均速度与ABCDE段的平均速度相同 |
12.一汽车在公路上行驶,位移和速度关系为x=40-$\frac{{v}^{2}}{10}$,其中x单位为m,v单位为m/s.则下列说法正确的是( )
| A. | 汽车做减速运动,初速度大小为10m/s2 | |
| B. | 汽车做减速运动,加速度大小为5m/s2 | |
| C. | 汽车经过4s速度减小到零 | |
| D. | 汽车经过2s速度减小到零 |
 如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大?
如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大?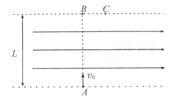 如图所示,在宽度为L的条形区域内有匀强电场,电场的方向平行于区域边界,一个带电粒子从下边界上的A点,以初速度v0沿垂直于电场的AB方向射入电场,从上边界的C点射出.已知粒子的重力不计,上边界上BC间距离为$\frac{1}{4}$L.
如图所示,在宽度为L的条形区域内有匀强电场,电场的方向平行于区域边界,一个带电粒子从下边界上的A点,以初速度v0沿垂直于电场的AB方向射入电场,从上边界的C点射出.已知粒子的重力不计,上边界上BC间距离为$\frac{1}{4}$L.