题目内容
4.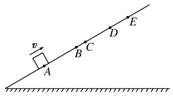 如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )
如图所示,一小滑块(可视为质点)沿足够长的光滑斜面以初速度v向上做匀变速直线运动,依次经A、B、C、D到达最高点E,然后又以相同的加速度从E点回到A点,已知AB=BD,BC=1m,滑块在上滑过程中从A到C和从C到D所用的时间相等,滑块两次经过A点的时间为16s,两次经过D点的时间为8s.则( )| A. | 通过A点的速率为8 m/s | B. | 通过B点的速率为$\sqrt{10}$ m/s | ||
| C. | 通过C点的速率为6 m/s | D. | CD:DE=5:4 |
分析 根据运动的对称性分别求出A到E和D到E的实际,抓住A到C和C到D的时间,得出相等的时间,结合连续相等时间内的位移之差是一恒量求出加速度,采用逆向思维,结合速度时间公式求出A、D的速度,根据速度时间公式求出C点的速度,运用速度位移公式求出B点的速度.根据速度位移公式求出CD和DE的距离,从而得出位移之比.
解答 解:A、滑块两次经过A点的时间为16s,两次经过D点的时间为8s,根据对称性知,滑块从A到E的时间为8s,同理,滑块从D到E的时间为4s,则A到D的时间为4s,因为A到C和C到D的时间相等,均为2s,根据${x}_{CD}-{x}_{AC}=a{T}^{2}$得,加速度a=$\frac{{x}_{CD}-{x}_{AC}}{{T}^{2}}$=-$\frac{2}{4}=-0.5m/{s}^{2}$,采用逆向思维,则通过A点的速率vA=at1=0.5×8m/s=4m/s,故A错误.
B、C点的速率vC=vA+at2=4-0.5×2m/s=3m/s,根据速度位移公式得,${{v}_{C}}^{2}-{{v}_{B}}^{2}=2a{x}_{BC}$,解得${v}_{B}=\sqrt{{{v}_{C}}^{2}-2a{x}_{BC}}$=$\sqrt{9+2×0.5×1}$m/s=$\sqrt{10}$m/s,故B正确,C错误.
D、D点的速率vD=at′=0.5×4m/s=2m/s,则CD间的距离${x}_{CD}=\frac{{{v}_{D}}^{2}-{{v}_{C}}^{2}}{2a}=\frac{4-9}{-1}m=5m$,DE间的距离${x}_{DE}=\frac{0-{{v}_{D}}^{2}}{2a}=\frac{0-4}{-1}m=4m$,则CD:DE=5:4,故D正确.
故选:BD.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,注意逆向思维在运动学中的应用.

| A. | 相应的运动距离之比一定是S1:S2:S3:…=1:4:9:… | |
| B. | 相邻的相同时间内的位移之比一定是S1:S2:S3:…=1:3:5:… | |
| C. | 相邻的相同时间内位移之差值一定是△S=aT2,其中T为相同的时间间隔 | |
| D. | t1、t2、t3秒末的速度之比一定是v1:v2:v3:…=1:2:3:… |
| A. | 无论B车匀加速的加速度值为多少,s是相同的 | |
| B. | 乘客甲节约的5个站的减速、停车、加速时间 | |
| C. | 若B车匀加速的时间为1min,则s为4km | |
| D. | 若B车匀减速的加速度大小为5m/s2,则当B车停下时A车距随州站的距离为1km |
 如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则此时( )
如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为Ff,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则此时( )| A. | 人拉绳行走的速度为vsin θ | B. | 人拉绳行走的速度为vcos θ | ||
| C. | 船的加速度为$\frac{Fcosθ-{F}_{f}}{m}$ | D. | 船的加速度为$\frac{F-{F}_{f}}{m}$ |
 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )| A. | 卫星甲的周期最大 | |
| B. | 卫星甲、乙经过P点时的加速度大小相等 | |
| C. | 三个卫星在远地点的速度可能大于第一宇宙速度 | |
| D. | 如果地球自转的角速度突然变为原来的$\frac{(g+a)}{a}$倍,那么赤道上的物体将会“飘”起来 |
| A. | 该行星的第一宇宙速度为$\frac{πR}{T}$ | |
| B. | 宇宙飞船绕该星球做圆周运动的周期不小于πt$\sqrt{\frac{2R}{h}}$ | |
| C. | 该行星的平均密度为$\frac{3π}{{T}^{2}G}$ | |
| D. | 如果该行星存在一颗同步卫星,其距行星表面高度为$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$-R |
 如图所示是某次实验中获得的小球下落时的频闪照片,频闪间隔是$\frac{1}{30}$s.根据此照片计算小球在4.90cm位置处的速度大小为0.984m/s;小球下落的加速度大小为9.77m/s2.(结果保留3位有效数字)
如图所示是某次实验中获得的小球下落时的频闪照片,频闪间隔是$\frac{1}{30}$s.根据此照片计算小球在4.90cm位置处的速度大小为0.984m/s;小球下落的加速度大小为9.77m/s2.(结果保留3位有效数字)
 小物块从斜面最低点D以v0=4m/s的速度滑上光滑的斜面,途经A、B两点,已知物体在A点时的速度是B点时的速度的2倍,由B点再经0.5s物块滑到斜面顶点C速度变为零,A、B的距离s=0.75m,已知小物块在斜面上运动的加速度恒定且沿斜面向下,小物块视为质点,求:
小物块从斜面最低点D以v0=4m/s的速度滑上光滑的斜面,途经A、B两点,已知物体在A点时的速度是B点时的速度的2倍,由B点再经0.5s物块滑到斜面顶点C速度变为零,A、B的距离s=0.75m,已知小物块在斜面上运动的加速度恒定且沿斜面向下,小物块视为质点,求: