题目内容
2.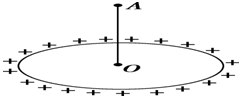 如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.
如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为r,放在绝缘水平桌面上.圆心为O点,过O点作一竖直线,在此线上取一点A,使A到O点的距离为0.75r,在A点放一检验电荷-q,则-q在A点所受的库仑力大小为$\frac{48kQq}{125{r}^{2}}$.
分析 把检验电荷受的力分解为沿竖直线和垂直于竖直线,由电荷的对称性知垂直于竖直线方向的力相互抵消,从而即可求解.
解答 解:检验电荷受的库仑力沿着电荷的连线指向+q,由对称性可知在垂直于竖直线的方向上的分力相互抵消,只有沿竖直线方向的分力.
由库仑力公式知:F=k$\frac{Qq}{{r}^{2}+(\frac{3r}{4})^{2}}$ cos53°=$\frac{48kQq}{125{r}^{2}}$,
故答案为:$\frac{48kQq}{125{r}^{2}}$.
点评 画出受力图,利用力的分解可以顺利解出本题,同时掌握库仑定律及力的矢量合成法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.高铁专家正设想一种“遇站不停式匀速循环运行”列车,如襄阳→随州→武汉→仙桃→潜江→荆州→荆门→襄阳,构成7站铁路圈,建两条靠近的铁路环线,列车A以恒定速率360km/h运行在一条铁路上,另一条铁路上有“伴驳列车”B,如某乘客甲想从襄阳站上车到潜江站,先在襄阳站登上B车,当A车快到襄阳站且距襄阳站的路程为s处时,B车从静止开始做匀加速运动,当速度达到360km/h时恰好遇到A车,两车连锁并打开乘客双向通道,A、B列车交换部分乘客,并连体运动一段时间再解锁分离,B车匀减速运动后停在随州站并缷客,A车上的乘客甲可以中途不停站直达潜江站,则( )
| A. | 无论B车匀加速的加速度值为多少,s是相同的 | |
| B. | 乘客甲节约的5个站的减速、停车、加速时间 | |
| C. | 若B车匀加速的时间为1min,则s为4km | |
| D. | 若B车匀减速的加速度大小为5m/s2,则当B车停下时A车距随州站的距离为1km |
13. 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切,以下说法中正确的是( )| A. | 卫星甲的周期最大 | |
| B. | 卫星甲、乙经过P点时的加速度大小相等 | |
| C. | 三个卫星在远地点的速度可能大于第一宇宙速度 | |
| D. | 如果地球自转的角速度突然变为原来的$\frac{(g+a)}{a}$倍,那么赤道上的物体将会“飘”起来 |
10.节日燃放礼花弹时,要先将礼花弹放入一个竖直的炮筒中,然后点燃礼花弹的发射部分,通过火药剧烈燃烧产生的高压气体,将礼花弹由炮筒底部射向空中.若礼花弹在由炮筒底部出发至炮筒口的过程中质量不变,克服重力做功W1,克服炮筒阻力及空气阻力做功W2,高压燃气对礼花弹做功W3,则礼花弹在炮筒内运动的过程中( )
| A. | 礼花弹的动能变化量为W3-W2-W1 | B. | 礼花弹的动能变化量为W3+W2+W1 | ||
| C. | 礼花弹的机械能变化量为W3-W1 | D. | 礼花弹的机械能变化量为W3-W2-W1 |
17. 如图所示,在倾角为30°的粗糙斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{1}{2}$g(g为重力加速度)向上加速运动距离s的过程中,下列说法正确的( )
如图所示,在倾角为30°的粗糙斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{1}{2}$g(g为重力加速度)向上加速运动距离s的过程中,下列说法正确的( )
 如图所示,在倾角为30°的粗糙斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{1}{2}$g(g为重力加速度)向上加速运动距离s的过程中,下列说法正确的( )
如图所示,在倾角为30°的粗糙斜面上,质量为m的物块在恒定拉力作用下沿斜面以加速度a=$\frac{1}{2}$g(g为重力加速度)向上加速运动距离s的过程中,下列说法正确的( )| A. | 重力势能增加mgs | B. | 动能增加mgs | C. | 机械能增加mgs | D. | 拉力做功为mgs |
7. 平行板电容器的两极板A、B接于电源两极,两极板竖直、平行正对.一带电小球悬挂在电容器内部,闭合开关S,电容器充电,悬线静止时偏离竖直方向的夹角为θ,如图所示.则下列说法正确的是( )
平行板电容器的两极板A、B接于电源两极,两极板竖直、平行正对.一带电小球悬挂在电容器内部,闭合开关S,电容器充电,悬线静止时偏离竖直方向的夹角为θ,如图所示.则下列说法正确的是( )
 平行板电容器的两极板A、B接于电源两极,两极板竖直、平行正对.一带电小球悬挂在电容器内部,闭合开关S,电容器充电,悬线静止时偏离竖直方向的夹角为θ,如图所示.则下列说法正确的是( )
平行板电容器的两极板A、B接于电源两极,两极板竖直、平行正对.一带电小球悬挂在电容器内部,闭合开关S,电容器充电,悬线静止时偏离竖直方向的夹角为θ,如图所示.则下列说法正确的是( )| A. | 开关S闭合,将A板向B板靠近,则θ减小 | |
| B. | 开关S闭合,将A板向B板靠近,则θ增大 | |
| C. | 开关S断开,将A板向B板靠近,则θ增大 | |
| D. | 开关S断开,将A板向B板靠近,则θ不变 |
14.据报道,美国国家航空航天局宣布首次在太阳系外发现“类地”行星,假如宇航员乘坐宇宙飞船到达该行星,进行科学观测,得到该行星的自转周期为T;宇航员在该行星“北极”距该行星地面附近h处自由释放一个小球(引力视为恒力),落地时间为t.已知该行星半径为R,万有引力常量为G,则下列说法正确的是( )
| A. | 该行星的第一宇宙速度为$\frac{πR}{T}$ | |
| B. | 宇宙飞船绕该星球做圆周运动的周期不小于πt$\sqrt{\frac{2R}{h}}$ | |
| C. | 该行星的平均密度为$\frac{3π}{{T}^{2}G}$ | |
| D. | 如果该行星存在一颗同步卫星,其距行星表面高度为$\root{3}{\frac{h{T}^{2}{R}^{2}}{2{π}^{2}{t}^{2}}}$-R |
12.一汽车在公路上行驶,位移和速度关系为x=40-$\frac{{v}^{2}}{10}$,其中x单位为m,v单位为m/s.则下列说法正确的是( )
| A. | 汽车做减速运动,初速度大小为10m/s2 | |
| B. | 汽车做减速运动,加速度大小为5m/s2 | |
| C. | 汽车经过4s速度减小到零 | |
| D. | 汽车经过2s速度减小到零 |
 如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大?
如图所示,一个质量m的物体,从倾角为θ,高为h的斜面上端A点,由静止开始下滑,到B点时的速度为v,然后又在水平面上滑行s位移后停止在C点,物体从A点开始下滑到B点的过程中克服摩擦力所做的功为多少?物体与水平面间的动摩擦系数为多大?