题目内容
11.两个物体A、B,以相同的速率V0在同一位置时向相反的方向水平抛出,经时间t,A的速度方向与B的位移方向相互垂直,则t为:( )| A. | $\frac{{V}_{0}}{g}$ | B. | $\frac{2{V}_{0}}{g}$ | C. | $\frac{{V}_{0}}{2g}$ | D. | $\frac{\sqrt{2}{V}_{0}}{g}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,结合A的速度方向与B的位移方向相互垂直求出运动的时间.
解答 解:两球以相同的初速度向相反方向做平抛运动,任何一时刻,两球在同一位置,速度方向与水平方向的夹角相等,位移方向与水平方向的夹角相等,
某时刻速度方向与水平方向的夹角正切值是位移与水平方向夹角正切值的2倍,因为α+β=90°,
tanα=2tanβ=2tan(90°-α),
即:$tanα=\sqrt{2}$,
根据$tanα=\frac{gt}{{v}_{0}}=\sqrt{2}$得:
t=$\frac{\sqrt{2}{v}_{0}}{g}$.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动的推论:某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径R和公转周期T,已知引力常量为G,由此可算出( )
| A. | 恒星质量 | B. | 恒星平均密度 | C. | 行星质量 | D. | 行星半径 |
6. 如图所示,一滑雪运动员以一定的初速度从一平台上A点滑出,落在斜坡上的B点时,其速度方向刚好沿着斜面向下,设平台边缘A点与斜坡B点连线与竖直方向之间的夹角为α,斜坡倾角为β,则( )
如图所示,一滑雪运动员以一定的初速度从一平台上A点滑出,落在斜坡上的B点时,其速度方向刚好沿着斜面向下,设平台边缘A点与斜坡B点连线与竖直方向之间的夹角为α,斜坡倾角为β,则( )
 如图所示,一滑雪运动员以一定的初速度从一平台上A点滑出,落在斜坡上的B点时,其速度方向刚好沿着斜面向下,设平台边缘A点与斜坡B点连线与竖直方向之间的夹角为α,斜坡倾角为β,则( )
如图所示,一滑雪运动员以一定的初速度从一平台上A点滑出,落在斜坡上的B点时,其速度方向刚好沿着斜面向下,设平台边缘A点与斜坡B点连线与竖直方向之间的夹角为α,斜坡倾角为β,则( )| A. | $\frac{tanα}{tanβ}$=2 | B. | $\frac{tanβ}{tanα}$=2 | C. | tanα•tanβ=1 | D. | tanα•tanβ=2 |
16. 2000年1月26日我国反射了一颗地球同步卫星,其定点位置与东经98°的经线在同一平面内,如图所示,反射地球同步卫星时,先将卫星发射至近地圆轨道1;然后点火,使其沿椭圆轨道2运行;最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点.轨道2、3相切于P点.当卫星分别在l、2、3轨道上正常运行时( )
2000年1月26日我国反射了一颗地球同步卫星,其定点位置与东经98°的经线在同一平面内,如图所示,反射地球同步卫星时,先将卫星发射至近地圆轨道1;然后点火,使其沿椭圆轨道2运行;最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点.轨道2、3相切于P点.当卫星分别在l、2、3轨道上正常运行时( )
 2000年1月26日我国反射了一颗地球同步卫星,其定点位置与东经98°的经线在同一平面内,如图所示,反射地球同步卫星时,先将卫星发射至近地圆轨道1;然后点火,使其沿椭圆轨道2运行;最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点.轨道2、3相切于P点.当卫星分别在l、2、3轨道上正常运行时( )
2000年1月26日我国反射了一颗地球同步卫星,其定点位置与东经98°的经线在同一平面内,如图所示,反射地球同步卫星时,先将卫星发射至近地圆轨道1;然后点火,使其沿椭圆轨道2运行;最后再次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点.轨道2、3相切于P点.当卫星分别在l、2、3轨道上正常运行时( )| A. | 若设卫星在轨道1上的速率v1、卫星在轨道3上的速率v3,则v1<v3. | |
| B. | 若设卫星在轨道1上经过Q点的加速度为a1Q;卫星在轨道2上经过Q点时的加速度为a2Q,则a1Q<a2Q. | |
| C. | 卫星要由轨道1变轨道2,需要在Q点加速 | |
| D. | 位置由轨道2变轨进入轨道3需要减速 |
20.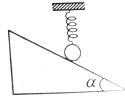 竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
 竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )
竖直弹簧的下端悬挂一小球,静止时,弹簧对小球的拉力大小为T.现使小球靠着倾角为α的光滑斜面,弹簧仍保持竖直,且整个装置处于静止状态,如图所示,则小球对斜面的压力大小为( )| A. | T | B. | 0 | C. | Tcosα | D. | Ttanα |
11.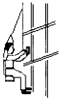 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
 如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )
如图所示,清洗楼房玻璃的工人常用一根绳索将自己悬在空中,工作及其装备的总重量为G,绳索与竖直墙壁的夹角为α,绳索对工人的拉力大小为F1,墙壁对工人的弹力大小为F2,假定工人上升时姿式保持不变,不计一切摩擦及绳索的重力,则( )| A. | F1=$\frac{G}{sinα}$ | |
| B. | F2=$\frac{G}{sinα}$ | |
| C. | 若缓慢减小绳索的长度,F1与F2的合力变大 | |
| D. | 若缓慢减小绳索的长度,F1与F2都增大 |
 在“用油膜法估测分子大小”的实验中,首先要确定一滴油酸酒精溶液中纯油酸的体积,具体做法是:把浓度为η的油酸酒精溶液一滴一滴地滴入量筒,记下滴入溶液滴数n时、量筒内增加的体积为V,则一滴溶液中纯油酸的体积为$\frac{Vη}{n}$;然后将一滴油酸酒精溶液滴入盛水的浅盘里,待水面稳定后,记下如图油酸分布图,已知图中每个正方形小方格的面积为S0.则油酸分子直径大小的表达式为$\frac{Vη}{57n{S}_{0}}$.
在“用油膜法估测分子大小”的实验中,首先要确定一滴油酸酒精溶液中纯油酸的体积,具体做法是:把浓度为η的油酸酒精溶液一滴一滴地滴入量筒,记下滴入溶液滴数n时、量筒内增加的体积为V,则一滴溶液中纯油酸的体积为$\frac{Vη}{n}$;然后将一滴油酸酒精溶液滴入盛水的浅盘里,待水面稳定后,记下如图油酸分布图,已知图中每个正方形小方格的面积为S0.则油酸分子直径大小的表达式为$\frac{Vη}{57n{S}_{0}}$. 某同学利用竖直上抛小球的频闪照片“验证机械能守恒定律”.频闪仪每隔0.05s闪光一次,照片的一部分如图所示.图中所标数据为实际距离.小球的质量m=0.20kg,当地重力加速度取9.8m/s2,计算结果保留三位有效数字
某同学利用竖直上抛小球的频闪照片“验证机械能守恒定律”.频闪仪每隔0.05s闪光一次,照片的一部分如图所示.图中所标数据为实际距离.小球的质量m=0.20kg,当地重力加速度取9.8m/s2,计算结果保留三位有效数字