题目内容
2.如图所示,两足够长的平行光滑的金属导轨MN、PQ相距L=1m,导轨平面与水平面夹角α=30°.磁感应强度为B1=2T的匀强磁场垂直导轨平面向上,长为L=1m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m1=2kg,电阻R1=1Ω.两金属导轨的上端连接右侧电路,通过导线接一对水平放置的平行金属板,两板间的距离和板长均为d=0.5m,定值电阻为R2=3Ω,现闭合开关S并将金属棒由静止释放,取g=10m/s2,导轨电阻忽略不计.则:
(1)金属棒下滑的最大速度为多大?
(2)当金属棒下滑达到稳定状态时,水平放置的平行金属板间电场强度是多大?
(3)当金属棒下滑达到稳定状态时,在水平放置的平行金属扳间加一垂直于纸面向里的匀强磁场B2=3T,在下板的右端且非常靠近下板的位置有一质量为m2、带电量为q=-1×10-4C的微粒以某一初速度水平向左射入两板间,要使该带电粒子在磁场中恰好做匀速圆周运动并能从金属板间射出,该微粒的初速度应满足什么条件?
分析 (1)当金属棒匀速运动时速度达到最大,此时 金属棒所受合力为零,由平衡条件可以求出最大速度.
(2)金属棒匀速运动时达到稳定状态,由欧姆定律求出极板间的电压,然后求出极板间的电场强度.
(3)微粒在极板间做匀速圆周运动,重力与电场力合力为零,洛伦兹力提供向心力,求出微粒从极板间射出的临界速度,然后确定其速度范围.
解答 解:(1)当金属棒匀速下滑时速度达到最大,
此时,感应电动势:E=B1Lvm,
感应电流:I=$\frac{E}{{R}_{1}+{R}_{2}}$=$\frac{{B}_{1}L{v}_{m}}{{R}_{1}+{R}_{2}}$,
导体棒匀速运动,处于平衡状态,
由平衡条件得:m1gsinα=B1IL,
解得:vm=$\frac{{m}_{1}g({R}_{1}+{R}_{2})sinα}{{B}_{1}^{2}{L}^{2}}$=$\frac{2×10×(1+3)sin30°}{{2}^{2}×{1}^{2}}$=10m/s;
(2)两极板间的电压:U=IR2=$\frac{{B}_{1}L{v}_{m}{R}_{2}}{{R}_{1}+{R}_{2}}$=$\frac{2×1×10×3}{1+3}$=15V,
两极板间电场强度:E=$\frac{U}{d}$=$\frac{15V}{0.5m}$=30V/m,方向:竖直向下;
(3)微粒做匀速圆周运动,重力与电场力合力为零,洛伦兹力提供向心力,
电场力与重力等大反向:qE=m2g,
由牛顿第二定律得:qvB2=m2$\frac{{v}^{2}}{r}$,解得:r=$\frac{{m}_{2}v}{q{B}_{2}}$,
微粒从金属板右侧射出需要满足:r≤$\frac{d}{2}$,
微粒从金属板左侧射出需要满足:r≥d,
解得:v≤0.25m/s或v≥0.5m/s;
答:(1)金属棒下滑的最大速度为10m/s;
(2)当金属棒下滑达到稳定状态时,水平放置的平行金属板间电场强度大小为:30V/m,方向:竖直向下;
(3)该微粒的初速度应满足的条件是:v≤0.25m/s或v≥0.5m/s.
点评 本题考查了带电微粒在磁场中的运动,考查了电磁感应现象,分析清楚金属棒的运动过程是解题的关键;求最后一问时考虑问题要全面,考虑微粒从左侧与从右侧射出两种情况,否则会漏解.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 第三届世界互联网大会将于2016年11月16日至18日在桐乡乌镇举办.为迎接大会的召开,桐乡市对乌镇部分道路亮化工程进行了改造,如图所示是乌镇某村使用的太阳能路灯的电池板铭牌,但由于某种原因,该电池板的工作电流没标上去,则它的数值大约为( )
第三届世界互联网大会将于2016年11月16日至18日在桐乡乌镇举办.为迎接大会的召开,桐乡市对乌镇部分道路亮化工程进行了改造,如图所示是乌镇某村使用的太阳能路灯的电池板铭牌,但由于某种原因,该电池板的工作电流没标上去,则它的数值大约为( )| A. | 4.65A | B. | 5.67 A | C. | 5.85A | D. | 6.67A |

| A. | 质点振动的周期T=0.2 s | |
| B. | 波速v=20 m/s | |
| C. | 因为一个周期质点运动0.8 m,所以波长λ=0.8 m | |
| D. | 从该时刻起经过0.15 s,波沿x轴正方向传播了3 m | |
| E. | 从该时刻起经过0.25 s时,质点Q的加速度大于质点P的加速度 |
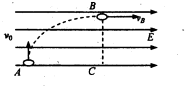 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
 在水平地面上,A、B两物体叠放如图所示,在水平力F的作用下一起匀速运动,若将水平力F作用在A上,两物体可能发生的情况是( )
在水平地面上,A、B两物体叠放如图所示,在水平力F的作用下一起匀速运动,若将水平力F作用在A上,两物体可能发生的情况是( )| A. | A、B一起匀速运动 | B. | A加速运动B静止 | ||
| C. | A加速运动,B匀速运动 | D. | .A与B一起加速运动 |
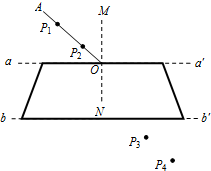 如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r.
如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r. 如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的无限大匀强磁场,质量为m、电荷量为+q的粒子1在纸面内以速度v0从O点射入磁场,其方向与MN的夹角α=30°;质量为m、电荷量为-q(q>0)的粒子2在纸面内也从O点沿相同的方向射入磁场,其速度大小也为v0.已知粒子1、2同时到达磁场边界的A、B两点离开磁场(图中未画出),不计粒子的重力及粒子间的相互作用.求:
如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的无限大匀强磁场,质量为m、电荷量为+q的粒子1在纸面内以速度v0从O点射入磁场,其方向与MN的夹角α=30°;质量为m、电荷量为-q(q>0)的粒子2在纸面内也从O点沿相同的方向射入磁场,其速度大小也为v0.已知粒子1、2同时到达磁场边界的A、B两点离开磁场(图中未画出),不计粒子的重力及粒子间的相互作用.求: 在用插针法“测定玻璃的折射率”的实验中,某同学用半圆形玻璃砖完成实验.如图所示,该同学先在平铺的白纸上画出直线MN,放好玻璃砖(图中实线部分),并在玻璃砖的一侧垂直纸面插上大头针G1、G2,以确定入射光线,让入射光线通过玻璃砖的圆心0;在玻璃砖的另一侧进行观察,调整视线,同时垂直纸面插上大头针G3,使G3挡住G1、G2的像;取走玻璃砖,标出大头针的位置,连接OG3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点.设AB的长度为L1,AO的长度为L2,CD的长度为L3,DO的长度为L4,为较方便地表示出玻璃砖的折射率,需用刻度尺测量L1、L3(用上述给出的字母表示),玻璃砖的折射率可表示为$\frac{{L}_{1}}{{L}_{3}}$.
在用插针法“测定玻璃的折射率”的实验中,某同学用半圆形玻璃砖完成实验.如图所示,该同学先在平铺的白纸上画出直线MN,放好玻璃砖(图中实线部分),并在玻璃砖的一侧垂直纸面插上大头针G1、G2,以确定入射光线,让入射光线通过玻璃砖的圆心0;在玻璃砖的另一侧进行观察,调整视线,同时垂直纸面插上大头针G3,使G3挡住G1、G2的像;取走玻璃砖,标出大头针的位置,连接OG3.图中MN为分界面,虚线半圆与玻璃砖对称,B、C分别是入射光线、折射光线与圆的交点,AB、CD均垂直于法线并分别交法线于A、D点.设AB的长度为L1,AO的长度为L2,CD的长度为L3,DO的长度为L4,为较方便地表示出玻璃砖的折射率,需用刻度尺测量L1、L3(用上述给出的字母表示),玻璃砖的折射率可表示为$\frac{{L}_{1}}{{L}_{3}}$. 如图所示,环形区域内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,内圆半径为R,外圆半径为(1+$\sqrt{2}$)R,两圆的圆心(重合)处不断向外发射电荷量为q、质量为m的带正电粒子,不计粒子所受重力及粒子间相互作用,粒子发射速度方向都水平向右,而速度大小都不同,导致一部分粒子从外圆飞出磁场,而另一部分粒子第一次出磁场是飞入内圆.
如图所示,环形区域内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,内圆半径为R,外圆半径为(1+$\sqrt{2}$)R,两圆的圆心(重合)处不断向外发射电荷量为q、质量为m的带正电粒子,不计粒子所受重力及粒子间相互作用,粒子发射速度方向都水平向右,而速度大小都不同,导致一部分粒子从外圆飞出磁场,而另一部分粒子第一次出磁场是飞入内圆.