题目内容
18.甲乙两个学习小组分别利用单摆测量重力加速度.
(1)甲组同学采用图所示的实验装置.
①利用单摆测重力加速度的实验中,为了减小测量周期的误差,应在平衡 位置开始计时和结束计时.
③在一次用单摆测定加速度的实验中,图A是用毫米刻度尺测摆长,若测得悬点到小球最下端长为h,小球直径为d,则摆长L=$h-\frac{d}{2}$.
图B为测量周期用的秒表,长针转一圈的时间为30s,表盘上部的小圆共15大格,每一大格为lmin,该单摆摆动n=50次全振动时,长、短针位置如图中所示,所用时间t=100.4s.用以上直接测量的L,t,n表示出重力加速度的计算式为g=$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$(不必代入具体数值).
③若某同学测摆长时,忘记测摆球的半径,而只把悬点到小球最下端长度作为摆长,则他根据以上计算式求得的重力加速度偏大(填“偏大”或“偏小”或“准确”)

(2)乙组同学在图C所示装置的基础上再增加一个速度传感器,如图D所示,将摆球拉开一小角度使其做简谐运动,速度传感器记录了摆球振动过程中速度随时间变化的关系,如图E所示的v-t图线.
①由图E可知,该单摆的周期T=2.0 s;
②更换摆线长度后,多次测量,根据实验数据,利用计算机作出T2-L(周期平方-摆长)图线,并根据图线拟合得到方程T2=4.04L+0.035.由此可以得出当地的重力加速度g=9.76m/s2.(取π2=9.86,结果保留3位有效数字) 若其他测量、计算均无误,则用上述方法算得的g值和真实值相比是不变的(选填“偏大”、“偏小”和“不变”.)
分析 (1)单摆测量重力加速度时,从平衡位置开始计时和结束计时,摆长等于摆线的长度和摆球半径之和;秒表的读数等于小盘读数加上大盘读数,根据单摆的周期公式求出单摆的重力加速度,结合摆长的测量误差得出重力加速度的测量误差.
(2)根据图线得出单摆的周期,根据T2-L的关系式,结合斜率求出重力加速度大小.
解答 解:(1)①利用单摆测重力加速度的实验中,为了减小测量周期的误差,应在平衡位置开始计时和结束计时;
②摆长等于摆线的长度到摆球球心的距离,摆长L=$h-\frac{d}{2}$;
秒表的小盘读数为90s,大盘读数为10.4s,则最终读数为100.4s;
单摆的周期T=$\frac{t}{n}$,根据T=$2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}=\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$.
③根据g=$\frac{4{π}^{2}L}{{T}^{2}}$知,测摆长时,忘记测摆球的半径,而只把悬点到小球最下端长度作为摆长,则摆长的测量值偏大,导致重力加速度的测量值偏大.
(2)①根据图线知,单摆的周期T=2.0s;
②根据T=$2π\sqrt{\frac{L}{g}}$得,${T}^{2}=\frac{4{π}^{2}L}{g}$,由T2=4.04L+0.035知,$\frac{4{π}^{2}}{g}=4.04$,解得g=9.76m/s2.
在T2-L图线中,求斜率时,未测量摆球的半径,不影响斜率的求解,则算出的g值和真实值相比是不变的.
故答案为:(1)①平衡,②$h-\frac{d}{2}$,100.4,$\frac{4{π}^{2}{n}^{2}L}{{t}^{2}}$,③偏大,(2)①2.0,9.76,不变.
点评 解决本题的关键知道实验的原理以及操作中的注意事项,知道重力加速度测量误差的来源,掌握图象法求解重力加速度的原理,难度中等.

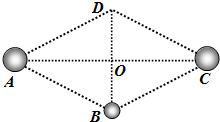 如图所示,ABCD为菱形的四个顶点,O为其中心,AC两点各固定有一个质量为M的球体,球心分别与AC两点重合,将一个质量为m的小球从B点由静止释放,只考虑M对m的引力作用,以下说法正确的有( )
如图所示,ABCD为菱形的四个顶点,O为其中心,AC两点各固定有一个质量为M的球体,球心分别与AC两点重合,将一个质量为m的小球从B点由静止释放,只考虑M对m的引力作用,以下说法正确的有( )| A. | m将在BD之间往复运动 | |
| B. | m从B到O的过程当中,做匀加速运动 | |
| C. | m从B到O的过程当中,左侧的M对m的引力越来越小 | |
| D. | m在整个运动过程中有三个位置所受合力的功率为零 |

| A. | 变压器输入、输出功率之比为4:1 | |
| B. | 变压器原、副线圈中的电流强度之比为1:4 | |
| C. | u随t变化的规律为u=51sin(50πt)(国际单位制) | |
| D. | 若热敏电阻RT的温度升高,则电压表的示数不变,电流表的示数变大 |
| A. | 在匀强电场中,场强处处相同,电势也处处相等 | |
| B. | 在正点电荷形成的电场中,离点电荷越远,电势越高,场强越小 | |
| C. | 在任何电场中,场强越大的地方,电势也越高 | |
| D. | 等量异种点电荷形成的电场中,取无限远处为电势零点,两电荷连线中点的电势为零,场强不为零 |
 如图所示,竖直平面内的轨道Ⅰ和Ⅱ都由两段细直杆连接而成,两轨道的长度相等,用相同的水平恒力F将穿在轨道最低点B的静止小球,分别沿Ⅰ和Ⅱ推至最高点A时,速率分别为v1、v2,力F的功率分别为P1、P2;所用时间分别为t1、t2;机械能增加量分别为△E1、△E2,假定小球在经过轨道转折点前后速度大小不变,且小球与Ⅰ、Ⅱ轨道间动摩擦因数相等,则( )
如图所示,竖直平面内的轨道Ⅰ和Ⅱ都由两段细直杆连接而成,两轨道的长度相等,用相同的水平恒力F将穿在轨道最低点B的静止小球,分别沿Ⅰ和Ⅱ推至最高点A时,速率分别为v1、v2,力F的功率分别为P1、P2;所用时间分别为t1、t2;机械能增加量分别为△E1、△E2,假定小球在经过轨道转折点前后速度大小不变,且小球与Ⅰ、Ⅱ轨道间动摩擦因数相等,则( )| A. | P1>P2 | B. | t1<t2 | C. | △E1=△E2 | D. | v1>v2 |
| A. | 自然界中任何两个物体都相互吸引,引力的方向在它们的连线上 | |
| B. | 引力的大小与物体的质量m1和m2的乘积成正比,与它们之间的距离r成反比 | |
| C. | 万有引力公式中G为引力常量,它是由实验测得的,而不是人为规定的 | |
| D. | 引力常量G是由英国物理学家卡文迪许首先测出的 |
 如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=4kg的木板C置于木板B上,水平地面光滑,B.C之间存在摩擦,开始时B、C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回(A与B碰撞时间极短)(g=10m/s2),
如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=4kg的木板C置于木板B上,水平地面光滑,B.C之间存在摩擦,开始时B、C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回(A与B碰撞时间极短)(g=10m/s2), 如图所示,一个内壁光滑的绝热的圆柱形薄气缸,缸内有一个绝热活塞(活塞体积不计)将气缸分割成A、B两部分.活塞与桶壁无摩擦,不漏气.筒的顶部轻轻放上一质量与活塞K相等的导热性能良好的盖,盖与筒的上端边缘接触良好(无漏气缝隙).当B中气体温度t=27℃时,活塞上方A中盛有压强为pA=1.0×105Pa理想气体,下方B中盛有压强为pB=1.2×105Pa的理想气体,B中气体体积占总容积的$\frac{1}{10}$.现对B中气体缓慢加热,当达到平衡时,B中气体体积变为总容积的$\frac{2}{5}$.问B内气体温度t′是多少摄氏度?(已知到期压强为p0=1.0×105Pa.假设在加热过程中气缸与活塞K均不会被熔化,环境温度不变)
如图所示,一个内壁光滑的绝热的圆柱形薄气缸,缸内有一个绝热活塞(活塞体积不计)将气缸分割成A、B两部分.活塞与桶壁无摩擦,不漏气.筒的顶部轻轻放上一质量与活塞K相等的导热性能良好的盖,盖与筒的上端边缘接触良好(无漏气缝隙).当B中气体温度t=27℃时,活塞上方A中盛有压强为pA=1.0×105Pa理想气体,下方B中盛有压强为pB=1.2×105Pa的理想气体,B中气体体积占总容积的$\frac{1}{10}$.现对B中气体缓慢加热,当达到平衡时,B中气体体积变为总容积的$\frac{2}{5}$.问B内气体温度t′是多少摄氏度?(已知到期压强为p0=1.0×105Pa.假设在加热过程中气缸与活塞K均不会被熔化,环境温度不变)