��Ŀ����
4�� ��ͼ��ʾ������ǿ�ų�����һ��б��ƽ�н������죬������Ϊl�������������һ����R������ƽ����ˮƽ��ļн�Ϊ�ȣ���������ĵ�����Ϳ�б���ԵͿ�㣮��ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪB�������뵼��ƽ�洹ֱ������Ϊm�ĵ������h�߶ȴ��ɾ�ֹ�ͷţ��ڸ�Ҫ����Ϳ�㴦ʱǡ�������˶��������ʼ���뵼�촹ֱ�ҽ���Ϳ�����Ħ������Ħ��������=tan�ȣ��������ֵĵ��費�ƣ��������ٶ�Ϊg������˵����ȷ���ǣ�������
��ͼ��ʾ������ǿ�ų�����һ��б��ƽ�н������죬������Ϊl�������������һ����R������ƽ����ˮƽ��ļн�Ϊ�ȣ���������ĵ�����Ϳ�б���ԵͿ�㣮��ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪB�������뵼��ƽ�洹ֱ������Ϊm�ĵ������h�߶ȴ��ɾ�ֹ�ͷţ��ڸ�Ҫ����Ϳ�㴦ʱǡ�������˶��������ʼ���뵼�촹ֱ�ҽ���Ϳ�����Ħ������Ħ��������=tan�ȣ��������ֵĵ��費�ƣ��������ٶ�Ϊg������˵����ȷ���ǣ�������| A�� | ���������Ϳ��ǰ�����ٶȼ�С�ļ����˶� | |
| B�� | ��Ϳ����������������˶� | |
| C�� | ���������˵��ٶ�Ϊ$\frac{mgRsin��}{{B}^{2}{L}^{2}}$ | |
| D�� | �����˶������в����Ľ�����Ϊmgh-$\frac{{m}^{3}{g}^{2}si{n}^{2}��}{2{B}^{4}{L}^{4}}$ |
���� �о�������ھ�ԵͿ���������˶����̣�����ƽ�⣬����ƽ������������Ħ�������̣��������ڻ���Ϳ��֮ǰ�Ѿ��������˶����Ƶ������������ٶȵĹ�ϵ������ƽ����������ٶ�v��
��� �⣺A�����������Ϳ��ǰ�ٶ�Խ��Խ����E=BLv�ã���Ӧ�綯��Խ��Խ����I=$\frac{E}{R}$��F=BIL�ã����ܵİ�����Խ��Խ����F=mgsin��-BIL=ma�ã����ٶ�Խ��ԽС����A��ȷ��
B�������嵽��Ϳ��ʱ��������ƽ�⣬���ǵ���Ϳ���������ʧ�����������õ�������ƽ�⣬�ʵ��������˶�����B����
C����������ƽ�������ã�BIL=mgsin�ȣ��ã�$\frac{{B}^{2}{L}^{2}v}{R}=mgsin��$������v=$\frac{mgRsin��}{{B}^{2}{L}^{2}}$����C��ȷ��
D���������غ�����Ľ�����Q=mgh-$\frac{1}{2}m{v}^{2}$-mgsin��L=mgh-$\frac{{m}^{3}{g}^{2}si{n}^{2}��}{2{B}^{4}{L}^{4}}$-mgsin��L����D����
��ѡ��AC
���� ���⿼��ƽ��������Ӧ�ã�ע���Ӧ�綯�ƺͰ���������ⷽʽ�������е��Ѷȣ�

��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ
14�� ��ͼ��λ��x����ij��ĵ����ֱ��PQ�Ҳ�ĵ��Ʀ���x�仯��ͼ�ߣ�a��b��x���ϵ����㣬��P�㴹ֱ��x���ֱ��PQ��x���Ǹ����ߵĽ����ߣ�������˵����ȷ���ǣ�������
��ͼ��λ��x����ij��ĵ����ֱ��PQ�Ҳ�ĵ��Ʀ���x�仯��ͼ�ߣ�a��b��x���ϵ����㣬��P�㴹ֱ��x���ֱ��PQ��x���Ǹ����ߵĽ����ߣ�������˵����ȷ���ǣ�������
 ��ͼ��λ��x����ij��ĵ����ֱ��PQ�Ҳ�ĵ��Ʀ���x�仯��ͼ�ߣ�a��b��x���ϵ����㣬��P�㴹ֱ��x���ֱ��PQ��x���Ǹ����ߵĽ����ߣ�������˵����ȷ���ǣ�������
��ͼ��λ��x����ij��ĵ����ֱ��PQ�Ҳ�ĵ��Ʀ���x�仯��ͼ�ߣ�a��b��x���ϵ����㣬��P�㴹ֱ��x���ֱ��PQ��x���Ǹ����ߵĽ����ߣ�������˵����ȷ���ǣ�������| A�� | �����жϳ�OP��ĸ�����ƾ�Ϊ�� | |
| B�� | �����жϳ�a��ĵ糡ǿ��С��b��ĵ糡ǿ�� | |
| C�� | �����жϳ�P��������Ҳ�ĵ糡�����Ϊx�������� | |
| D�� | ����������a��ĵ�����С����b��ĵ����� |
12�������������ݲ����ڽ�������Чֵ���ǣ�������
| A�� | ���������ʾ�� | B�� | ���ݵĶ��ѹ | ||
| C�� | ����������ѹֵ | D�� | ����˿�Ķ���� |
19�� ��ͼ��ʾ��ˮƽ���ϵ�������ˮƽ���ҡ���СΪF���������ã����崦�ھ�ֹ״̬��������ô�С��ΪF��ˮƽ������������壬������
��ͼ��ʾ��ˮƽ���ϵ�������ˮƽ���ҡ���СΪF���������ã����崦�ھ�ֹ״̬��������ô�С��ΪF��ˮƽ������������壬������
 ��ͼ��ʾ��ˮƽ���ϵ�������ˮƽ���ҡ���СΪF���������ã����崦�ھ�ֹ״̬��������ô�С��ΪF��ˮƽ������������壬������
��ͼ��ʾ��ˮƽ���ϵ�������ˮƽ���ҡ���СΪF���������ã����崦�ھ�ֹ״̬��������ô�С��ΪF��ˮƽ������������壬������| A�� | ���崦�ھ�ֹ״̬���ܵ���Ħ������С���� | |
| B�� | ���崦�ھ�ֹ״̬���ܵ���Ħ������С | |
| C�� | ������ˮƽ�滬�����ܵ���Ħ������С���� | |
| D�� | ������ˮƽ�滬�����ܵ���Ħ������С |
16�� �����ɾ�ֹ��ʼ��ƽֱ�Ĺ�·����ʻ����0-40s�������ļ��ٶ���ʱ��仯��ͼ����ͼ��ʾ��������λ������ʱ���ǣ�������
�����ɾ�ֹ��ʼ��ƽֱ�Ĺ�·����ʻ����0-40s�������ļ��ٶ���ʱ��仯��ͼ����ͼ��ʾ��������λ������ʱ���ǣ�������
 �����ɾ�ֹ��ʼ��ƽֱ�Ĺ�·����ʻ����0-40s�������ļ��ٶ���ʱ��仯��ͼ����ͼ��ʾ��������λ������ʱ���ǣ�������
�����ɾ�ֹ��ʼ��ƽֱ�Ĺ�·����ʻ����0-40s�������ļ��ٶ���ʱ��仯��ͼ����ͼ��ʾ��������λ������ʱ���ǣ�������| A�� | 40sĩ | B�� | 30sĩ | C�� | 20sĩ | D�� | 10sĩ |

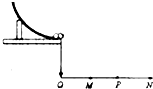 ��ͼ��ʾ������֤�����غ��ʵ���У�
��ͼ��ʾ������֤�����غ��ʵ���У�