题目内容
15.像打点计时器一样,光电计时器也是一种研究物体运动情况的常用计时仪器,其结构如图1所示.a、b分别是光电门的激光发射和接收装置,当有物体从a、b间通过时,光电计时器就可以显示物体的挡光时间.气垫导轨是常用的一种实验装置,它是利用气泵使带孔的导轨与滑块之间形成气垫,使滑块悬浮在导轨上,滑块在导轨上的运动可视为没有摩擦.我们可以用带光电门E、F的气垫导轨以及滑块A和B来验证动量守恒定律,实验装置如图2所示,(滑块A和B上的完全相同的挡光板未画出来),采用的实验步骤如下:
a.用天平分别测出滑块A、B的质量mA,mB
b.调整气垫导轨,使导轨处于水平
c.在A和B间放入一个被压缩的轻弹簧,用电动卡销锁定,静止放置在气垫导轨上
d.按下电钮放开卡销,光电门E、F各自连接的计时器显示的挡光时间分别为t1和t2.

(1)利用上述测量的实验数据,只要表达式$\frac{{m}_{A}}{△{t}_{1}}=\frac{{m}_{B}}{△{t}_{2}}$成立(用实验步骤中的物理量表示),就可以验证动量守恒定律.
(2)在本实验中,哪些因素可导致实验误差A.
A.导轨安放不水平
B.两滑块质量不相等
C.滑块上挡光板倾斜
D.滑块A和B上的挡光板宽度不严格相等
(3)利用上述实验数据测出被压缩弹簧的弹性势能的大小,还要测量的一个物理量是光板的宽度d.,请写出弹簧的弹性势能的表达式Ep=$\frac{{m}_{A}{d}^{2}}{2△{t}_{1}^{2}}+\frac{{m}_{B}{d}^{2}}{2△{t}_{2}^{2}}$.
分析 滑块的宽度除以滑块通过光电门的时间即为滑块通过光电门时的速度.
由于系统水平方向所受合外力为0,故系统水平方向动量守恒,在释放前系统的动量为0,故在释放后系统的动量仍然为0,则有mAv1+mB(-v2)=0.由机械能守恒定律可求得弹性势能的表达式.
解答 解:(1)滑块通过光电门E的速度为:v1=$\frac{d}{△{t}_{1}}$
滑块通过光电门F的速度为:v2=$\frac{d}{△{t}_{2}}$
由于系统水平方向所受合外力为0,故系统水平方向动量守恒,在释放前系统的动量为0,故在释放后系统的动量仍然为0,则有:
mAv1+mB(-v2)=0.
即:$\frac{{m}_{A}}{△{t}_{1}}=\frac{{m}_{B}}{△{t}_{2}}$成立,就可以验证动量守恒定律
(2)A.导轨安放不水平,则系统受到的合外力不为0,会影响实验的结果.故A符合题意;
B.两滑块质量不相等,则运动的时间不相等,由(1)的分析可知,对实验的结果没有影响,故B不符合题意;
C.滑块上挡光板倾斜不影响时间的测量,对实验的结果没有影响,故C不符合题意;
D.滑块A和B上的挡光板宽度不严格相等,由(1)的分析可知,与挡光板的宽度无关,对实验的结果没有影响,故D不符合题意.
故选:A
(3)根据机械能守恒定律可知系统的弹性势能转化为了两个物体的动能;故可以求出弹性势能的表达式;表达式为::EP=$\frac{1}{2}$mAv12+$\frac{1}{2}$mBv22=$\frac{{m}_{A}{d}^{2}}{2△{t}_{1}^{2}}+\frac{{m}_{B}{d}^{2}}{2△{t}_{2}^{2}}$
还要测量的一个物理量是挡光板的宽度d.
故答案为:(1)$\frac{{m}_{A}}{△{t}_{1}}=\frac{{m}_{B}}{△{t}_{2}}$;(2)A;(3)光板的宽度d.$\frac{{m}_{A}{d}^{2}}{2△{t}_{1}^{2}}+\frac{{m}_{B}{d}^{2}}{2△{t}_{2}^{2}}$
点评 本题考查动量守恒定律的实验验证;要注意通过认真审题明确实验原理,结合所学物理规律才能正确分析求解.

 木块的深度为d.为表示该过程,甲、乙两同学分别画出了如图所示的示意图.若子弹射入木块的时间极短,对于甲、乙两图的分析,下列说法中正确的是 ( )
木块的深度为d.为表示该过程,甲、乙两同学分别画出了如图所示的示意图.若子弹射入木块的时间极短,对于甲、乙两图的分析,下列说法中正确的是 ( )| A. | 当水平面光滑时甲图正确,当水平面粗糙时乙图正确 | |
| B. | 当子弹速度较大时甲图正确,当子弹速度较小时乙图正确 | |
| C. | 若水平面光滑,当M<m时,甲图正确,当M>m时乙图正确 | |
| D. | 不论水平面是否光滑,速度、质量大小关系如何,均是乙图正确 |
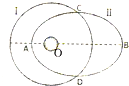 如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )
如图所示,曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图,其半径为R;曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图,O点为地球球心,AB为椭圆的长轴,两轨道和地心都在同一平面内,己知在两轨道上运动的卫星的周期相等,万有引力常量为G,地球质量为M,下列说法正确的是( )| A. | 椭圆轨道的长轴AB长度为R | |
| B. | 若OA=0.5R,则卫星在B点的速率vB<$\sqrt{\frac{2GM}{3R}}$ | |
| C. | 在Ⅰ轨道上卫星1的速率为v0,在Ⅱ轨道的卫星2在B点的速率为vB,则v0<vB | |
| D. | 两颗卫星运动到C点时,卫星1和卫星2的加速度不同 |
 如图所示,图甲已知力F和它的一个分力F1的大小和方向,图乙已知力F和两个分力的方向,关于该力F分解的正确说法是( )
如图所示,图甲已知力F和它的一个分力F1的大小和方向,图乙已知力F和两个分力的方向,关于该力F分解的正确说法是( )| A. | 甲和乙都能得到唯一的分解结果 | |
| B. | 甲和乙都不能得到唯一的分解结果 | |
| C. | 甲不能得到唯一的分解结果、乙能得到唯一的分解结果 | |
| D. | 甲能得到唯一的分解结果、乙不能得到唯一的分解结果 |
 如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )
如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )| A. | 导体棒到达涂层前做加速度减小的加速运动 | |
| B. | 在涂层区导体棒做减速运动 | |
| C. | 导体棒到达底端的速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| D. | 整个运动过程中产生的焦耳热为mgh-$\frac{{m}^{3}{g}^{2}si{n}^{2}θ}{2{B}^{4}{L}^{4}}$ |

 如图所示,AOB是光滑水平轨道,BC是半径为R的光滑的$\frac{1}{4}$固定圆弧轨道,两轨道恰好相切于B点.质量为M的小木块静止在O点,一个质量为m的子弹以某一初速度水平向右射入小木块内,并留在其中和小木块一起运动,且恰能到达圆弧轨道的最高点C(木块和子弹均可以看成质点).求:
如图所示,AOB是光滑水平轨道,BC是半径为R的光滑的$\frac{1}{4}$固定圆弧轨道,两轨道恰好相切于B点.质量为M的小木块静止在O点,一个质量为m的子弹以某一初速度水平向右射入小木块内,并留在其中和小木块一起运动,且恰能到达圆弧轨道的最高点C(木块和子弹均可以看成质点).求: