题目内容
19．
如图所示，水平面上的物体受水平向右、大小为F的拉力作用，物体处于静止状态．如果改用大小仍为F、水平向左的力推物体，则（ ）| A． | 物体处于静止状态，受到的摩擦力大小不变 | |
| B． | 物体处于静止状态，受到的摩擦力变小 | |
| C． | 物体沿水平面滑动，受到的摩擦力大小不变 | |
| D． | 物体沼水平面滑动，受到的摩擦力变小 |
分析 根据施力物体与受力物体、性质等分析物体对水平面的压力与物体的重力是否相同．分析物体受力情况，分析拉力F和水平面对物体的摩擦力的关系．
解答 解：物体水平方向受到拉力F和摩擦力而处于平衡状态，拉力F和水平面对物体的摩擦力是一对平衡力．
物体处于静止状态，受到的合外力为零，受到的摩擦力大小仍不变．故A正确，BCD错误．
故选：A．
点评 分析受力情况是学习力学的基本功，一般按重力、弹力和摩擦力的顺序分析，根据平衡条件：合力为零，分析各力的关系．
练习册系列答案
相关题目
9．
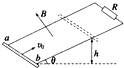如图所示，间距为L米的光滑平等金属轨道上端用电阻R相连，其平面与水平面成θ角，整个装置处于磁感应强度为B匀强磁场中，磁场方向垂直轨道平面向上，质量为m，电阻为r的金属杆ab（长度略大于L），以初速度v0从轨道底端向上滑行，滑行到距底端高h的位置后又返回到底端，运动过程中，金属杆始终与导轨垂直且接触良好，不计金属轨道的电阻，已知重力加速度为g，则以下说法正确的是（ ）
如图所示，间距为L米的光滑平等金属轨道上端用电阻R相连，其平面与水平面成θ角，整个装置处于磁感应强度为B匀强磁场中，磁场方向垂直轨道平面向上，质量为m，电阻为r的金属杆ab（长度略大于L），以初速度v0从轨道底端向上滑行，滑行到距底端高h的位置后又返回到底端，运动过程中，金属杆始终与导轨垂直且接触良好，不计金属轨道的电阻，已知重力加速度为g，则以下说法正确的是（ ）| A． | 杆ab先匀减速上滑，之后匀加速下滑，且上滑过程的加速度大于下滑过程的加速度 | |
| B． | 杆ab运动过程中安培力做功的功率等于电阻R的热功率 | |
| C． | 杆ab上滑过程中通过R的电荷量与下滑过程中通过R的电荷量相等 | |
| D． | 杆ab上滑到最高点的过程中电阻R上产生的焦耳热等于$\frac{R}{R+r}$（$\frac{1}{2}$mv02-mgh） |
10．
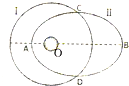如图所示，曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图，其半径为R；曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图，O点为地球球心，AB为椭圆的长轴，两轨道和地心都在同一平面内，己知在两轨道上运动的卫星的周期相等，万有引力常量为G，地球质量为M，下列说法正确的是（ ）
如图所示，曲线Ⅰ是绕地球做圆周运动卫星1的轨道示意图，其半径为R；曲线Ⅱ是绕地球做椭圆运动卫星2的轨道的示意图，O点为地球球心，AB为椭圆的长轴，两轨道和地心都在同一平面内，己知在两轨道上运动的卫星的周期相等，万有引力常量为G，地球质量为M，下列说法正确的是（ ）| A． | 椭圆轨道的长轴AB长度为R | |
| B． | 若OA=0.5R，则卫星在B点的速率vB＜$\sqrt{\frac{2GM}{3R}}$ | |
| C． | 在Ⅰ轨道上卫星1的速率为v0，在Ⅱ轨道的卫星2在B点的速率为vB，则v0＜vB | |
| D． | 两颗卫星运动到C点时，卫星1和卫星2的加速度不同 |
7．
如图所示，图甲已知力F和它的一个分力F1的大小和方向，图乙已知力F和两个分力的方向，关于该力F分解的正确说法是（ ）
如图所示，图甲已知力F和它的一个分力F1的大小和方向，图乙已知力F和两个分力的方向，关于该力F分解的正确说法是（ ）| A． | 甲和乙都能得到唯一的分解结果 | |
| B． | 甲和乙都不能得到唯一的分解结果 | |
| C． | 甲不能得到唯一的分解结果、乙能得到唯一的分解结果 | |
| D． | 甲能得到唯一的分解结果、乙不能得到唯一的分解结果 |
14．
如图所示，质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动．O为一光滑的孔，当拉力为F时，转动半径为R；当拉力增大到8F时，物体仍作匀速圆周运动，此时转动半径为$\frac{R}{2}$．在此过程中，拉力对物体做的功为（ ）
如图所示，质量为m的物体用细绳牵引着在光滑的水平面上作匀速圆周运动．O为一光滑的孔，当拉力为F时，转动半径为R；当拉力增大到8F时，物体仍作匀速圆周运动，此时转动半径为$\frac{R}{2}$．在此过程中，拉力对物体做的功为（ ）| A． | $\frac{7}{2}$FR | B． | $\frac{7}{4}$FR | C． | $\frac{3}{2}$FR | D． | 4FR |
4．
如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为l，两导轨间连有一电阻R，导轨平面与水平面的夹角为θ，在两虚线间的导轨上涂有薄绝缘涂层．匀强磁场的磁感应强度大小为B，方向与导轨平面垂直．质量为m的导体棒从h高度处由静止释放，在刚要滑到涂层处时恰好匀速运动．导体棒始终与导轨垂直且仅与涂层间有摩擦，动摩擦因数μ=tanθ，其他部分的电阻不计，重力加速度为g，下列说法正确的是（ ）
如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为l，两导轨间连有一电阻R，导轨平面与水平面的夹角为θ，在两虚线间的导轨上涂有薄绝缘涂层．匀强磁场的磁感应强度大小为B，方向与导轨平面垂直．质量为m的导体棒从h高度处由静止释放，在刚要滑到涂层处时恰好匀速运动．导体棒始终与导轨垂直且仅与涂层间有摩擦，动摩擦因数μ=tanθ，其他部分的电阻不计，重力加速度为g，下列说法正确的是（ ）| A． | 导体棒到达涂层前做加速度减小的加速运动 | |
| B． | 在涂层区导体棒做减速运动 | |
| C． | 导体棒到达底端的速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| D． | 整个运动过程中产生的焦耳热为mgh-$\frac{{m}^{3}{g}^{2}si{n}^{2}θ}{2{B}^{4}{L}^{4}}$ |
11．下列说法正确的是 （ ）
| A． | 天然放射现象的发现揭示了原子核有复杂的结构 | |
| B． | 氢原子从n=3的能级向低能级跃迁时只会辐射出两种不同频率的光 | |
| C． | 比结合能大的原子核分解成比结合能小的原子核时要吸收能量 | |
| D． | 放射性元素每经过一个半衰期，其质量减少一半 |
如图所示，质量M=20kg的工件放在水平地面上，工件上光滑斜面部分AB与水平部分BC的夹角为θ=37°，工件斜面与水平部分由一小段光滑圆弧连接，工件左侧与竖直墙壁之间固连一个力传感器，质量为m=10kg滑块（可看做质点），从A点由静止开始下滑，最后停在BC水平部分上，滑块整个运动时间为t=1.0s，工件与地面间的动摩擦因数为μ1=0.1，滑块与水平部分BC间的动摩擦因数μ2=0.4，整个过程中工件的水平位移忽略不计，工件与地面的最大静摩擦力等于滑动摩擦力（sin37°=0.6，cos37°=0.8），求：
9．
如图所示，粗糙的平行金属导轨倾斜放置，导轨电阻不计，顶端QQ′之间连接一个阻值为R的电阻和开关S，底端PP′处有一小段水平轨道相连，匀强磁场B垂直于导轨平面．断开开关S，将一根质量为m、长为l的金属棒从AA′处静止开始滑下，落在水平面上的FF′处；闭合开关S，将金属棒仍从AA′处静止开始滑下，落在水平面上的EE′处；开关S仍闭合，金属棒从CC′处静止开始滑下，仍落在水平面上的EE′处．（忽略金属棒经过PP′处的能量损失）测得相关数据如图所示，下列说法正确的是（ ）
如图所示，粗糙的平行金属导轨倾斜放置，导轨电阻不计，顶端QQ′之间连接一个阻值为R的电阻和开关S，底端PP′处有一小段水平轨道相连，匀强磁场B垂直于导轨平面．断开开关S，将一根质量为m、长为l的金属棒从AA′处静止开始滑下，落在水平面上的FF′处；闭合开关S，将金属棒仍从AA′处静止开始滑下，落在水平面上的EE′处；开关S仍闭合，金属棒从CC′处静止开始滑下，仍落在水平面上的EE′处．（忽略金属棒经过PP′处的能量损失）测得相关数据如图所示，下列说法正确的是（ ）| A． | S断开时，金属板沿斜面下滑的加速度$\frac{x_1^2g}{2hs}$ | |
| B． | B=$\frac{{x}_{1}}{2l}$$\root{4}{\frac{2{m}^{2}{R}^{2}g}{{s}^{2}{{x}_{2}}^{2}h}}$ | |
| C． | 电阻R上产生的热量Q=$\frac{mg}{4h}$（x12-x22） | |
| D． | CC′一定在AA′的上方 |