题目内容
12. 某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放手,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg.
某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放手,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg.(1)假设选手落到转盘上瞬间相对转盘速度立即变为零,为保证他落在任何位置都不会滑动,转盘的角速度ω应限制在什么范围?
(2)若选手从某处C点释放能恰好落到转盘的圆心上,求悬挂器从A点运动到C点所经历的时间.已知H=5m,L=8m,a=$\frac{2}{3}$m/s2,(g取10m/s2).
(3)当选手从A点开始运动时,盘边缘上P点刚好在最右端,问电动机产生的加速度a取哪些值,人可以落在P点?已知H=5m,L=8m,R=1m,ω=3.14rad/s,π取3.14,g取10m/s2.
分析 (1)根据静摩擦力提供向心力,结合牛顿第二定律求出转盘角速度的范围.
(2)抓住平抛运动的水平位移和匀加速直线运动的位移等于L,结合位移公式和速度公式求出匀加速运动的时间.
(3)结合(2)的分析,根据落在P点时,可能在O点的右侧,有可能在O点的左侧,结合速度位移公式即可求出.
解答 解:(1)设人落在距圆心最远R处不至被甩下,最大静摩擦力提供向心力,则有:
μmg≥mω2•R
即转盘转动的角速度满足ω≤$\sqrt{\frac{μg}{R}}$
(2)沿水平加速段位移为x1,时间为t1;平抛运动的水平位移为x2,时间为t2.
则加速时有${x}_{1}=\frac{1}{2}a{t}^{2}$
v=at1
平抛运动阶段x2=vt2
H=$\frac{1}{2}g{t}^{2}$
全程水平方向:x1+x2=L;
代入数据,联立各式解得t1=4s,t2=1s.
(3)当P在最右侧时:t=$\frac{2nπ}{ω}=2n$,
$\frac{1}{2}a(t-{t}_{2})^{2}+a(t-{t}_{2})•{t}_{2}=L+R$
联立得:a=$\frac{18}{4{n}^{2}-1}$(n=1,2,3…)
当P在最左侧时,t=$\frac{(2n-1)π}{ω}=2n-1$
$\frac{1}{2}a{(t-{t}_{2})}^{2}+a(t-{t}_{2})•{t}_{2}=L-R$
联立得:a=$\frac{7}{2{n}^{2}-2n}$(n=2,3,4…)
答:(1)假设选手落到转盘上瞬间相对转盘速度立即变为零,为保证他落在任何位置都不会滑动,转盘的角速度ω应;
(2)若选手从某处C点释放能恰好落到转盘的圆心上,悬挂器从A点运动到C点所经历的时间是4s.
(3)当选手从A点开始运动时,盘边缘上P点刚好在最右端,电动机产生的加速度a取$\frac{18}{4{n}^{2}-1}$(n=1,2,3…)或$\frac{7}{2{n}^{2}-2n}$(n=2,3,4…)时人可以落在P点.
点评 该题属于单物体多过程的情况,解决本题的关键理清选手的运动过程,结合牛顿第二定律和运动学公式灵活求解.

| A. | 冥王星绕太阳运行的周期一定大于地球的公转周期 | |
| B. | 冥王星绕太阳运行的最小加速度一定小于地球绕太阳运行的最小加速度 | |
| C. | 冥王星的密度一定小于地球的密度 | |
| D. | 冥王星表面的重力加速度一定小于地球表面的重力加速度 |
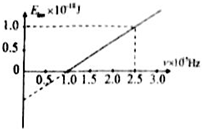 用某单色光照射金属钛表面,发生光电效应.从钛表面放出光电子的最大初动能与入射光频率的关系图线如图.已知普朗克常量为6.67×10-34J•s,则下列说法正确的是( )
用某单色光照射金属钛表面,发生光电效应.从钛表面放出光电子的最大初动能与入射光频率的关系图线如图.已知普朗克常量为6.67×10-34J•s,则下列说法正确的是( )| A. | 钛的逸出功为6.67×10-19J | |
| B. | 钛的极限频率为1.0×1015Hz | |
| C. | 光电子的最大初动能为1.0×10-18J | |
| D. | 用不同频率的单色光照射金属钛表面,若都能发生光电效应,则其最大初动能并不相同 | |
| E. | 光电子的最大初动能与入射光的频率成正比 |
 如图所示,甲、乙两种静止状态中,弹簧秤、绳子、滑轮的重力不计,绳子和滑轮摩擦也不计,物体的重力都是G.若弹簧秤的示数分别是F1、F2,则( )
如图所示,甲、乙两种静止状态中,弹簧秤、绳子、滑轮的重力不计,绳子和滑轮摩擦也不计,物体的重力都是G.若弹簧秤的示数分别是F1、F2,则( )| A. | F1>F2=G | B. | F1<F2=G | C. | F2>F1=G | D. | F1=F2=G |
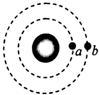
| A. | a、b线速度之比为3:2 | B. | a、b角速度之比为2$\sqrt{2}$:3$\sqrt{3}$ | ||
| C. | a、b周期之比为2$\sqrt{2}$:3$\sqrt{3}$ | D. | a、b向心加速度之比为4:9 |
 如图所示,质量分别为m1、m2的物体用一质量不计的轻绳连接,跨过固定在墙壁上的定滑轮O,其中质量为m1的物体穿过一竖直固定的杆,图中的P点与定滑轮在同一高度处,将连接体由图中的位置自由释放,质量为m1的物体最高运动到P点.如果所有的摩擦力都可忽略不计,则在质量为m1的物体从自由释放到运动到P点的过程中( )
如图所示,质量分别为m1、m2的物体用一质量不计的轻绳连接,跨过固定在墙壁上的定滑轮O,其中质量为m1的物体穿过一竖直固定的杆,图中的P点与定滑轮在同一高度处,将连接体由图中的位置自由释放,质量为m1的物体最高运动到P点.如果所有的摩擦力都可忽略不计,则在质量为m1的物体从自由释放到运动到P点的过程中( )| A. | 质量为m1的物体运动到P点的加速度大小为零 | |
| B. | 轻绳对质量为m1的物体所做的功在数值上与该物体增加的重力势能相等 | |
| C. | 质量为m2的物体的机械能先增加后减小 | |
| D. | 轻绳对质量为m2的物体做的功等于该物体减少的机械能 |
| A. | 起重机吊起物体匀速上升 | |
| B. | 在空中做“香蕉球”运动的足球 | |
| C. | 物体沿斜面匀速下滑 | |
| D. | 不计空气阻力,物体以一定的初速度冲上固定的光滑斜面 |
 一条船要在最短时间内渡过宽为100m的河,已知河水的流速v1与船离河岸的距离x变化的关系如图甲所示,船在静水中的速度v2与时间t的关系如图乙所示,则以下判断中正确的是( )
一条船要在最短时间内渡过宽为100m的河,已知河水的流速v1与船离河岸的距离x变化的关系如图甲所示,船在静水中的速度v2与时间t的关系如图乙所示,则以下判断中正确的是( )| A. | 船渡河的最短时间是20 s | B. | 船运动的轨迹可能是直线 | ||
| C. | 船在河水中作匀速运动 | D. | 船在河水中的最大速度是5 m/s |
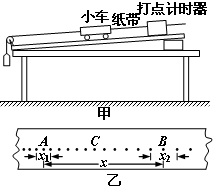 某实验小组采用如图甲所示的装置探究小车在 斜面上的运动情况.实验中重物通过跨过定滑轮的细绳带动小车,小车又带动纸带做匀变速直线运动,通过打点计时器在纸带上打下一系列点(如图乙所示).如果电磁打点计时器打点周期为T,测得图中的相应两点之间的距离x、x1、x2,则:
某实验小组采用如图甲所示的装置探究小车在 斜面上的运动情况.实验中重物通过跨过定滑轮的细绳带动小车,小车又带动纸带做匀变速直线运动,通过打点计时器在纸带上打下一系列点(如图乙所示).如果电磁打点计时器打点周期为T,测得图中的相应两点之间的距离x、x1、x2,则: