题目内容
15.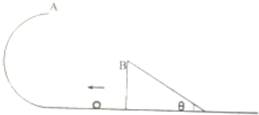 光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求:
光滑半圆弧槽竖直放置,半径为r=0.45m,斜面体高为h=0.45m,倾角为θ=37°,一小球质量为0.9kg,从水平面以某一速度滑入半圆弧槽,然后从顶端A点飞出,刚好从斜面顶端B点滑入斜面.(g=10m/s2)试求:(1)小球滑入B点时的速度.
(2)在A点,小球对圆弧槽的弹力.
分析 (1)球离开A后做平抛运动,应用平抛运动规律可以求出球滑入B点时的速度.
(2)在A点,小球做圆周运动,应用牛顿第二定律可以求出圆弧对球的支持力,然后求出球对圆弧的弹力.
解答 解:(1)小球离开A后做平抛运动,
竖直方向:vy2=2g(2r-h),
代入数据解得:vy=3m/s,
在B点,vB=$\frac{{v}_{y}}{sinθ}$=$\frac{3}{sin37°}$=5m/s;
(2)小球做平抛运动的水平速度:
vA=vBcosθ=5cos37°=4m/s,
在A点,由牛顿第二定律得:
F+mg=m$\frac{{v}_{A}^{2}}{r}$,代入数据解得:F=23N,
由牛顿第三定律可知,小球对轨道的弹力:F′=F=23N,方向:竖直向上;
答:(1)小球滑入B点时的速度大小为5m/s,方向沿斜面向下.
(2)在A点,小球对圆弧槽的弹力大小为23N,方向:竖直向上.
点评 本题考查了求速度与弹力问题,分析清楚小球的运动过程,应用平抛运动过程、运动的合成与分解、牛顿运动定律即可解题;要注意正确理解小球恰好沿斜面下滑的意义.

练习册系列答案
相关题目
3.关于抛体运动,下列说法不正确的是( )
| A. | 做平抛运动的物体运动方向逐渐靠近竖直方向,且速率不断变大,所以是变加速曲线运动 | |
| B. | 平抛运动中物体速度随时间变化是均匀的 | |
| C. | 类平抛运动可分解为初速度方向的匀速直线运动和与之垂直方向上的初速度为零的匀加速直线运动 | |
| D. | 斜抛运动是匀变速曲线运动 |
10. 甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
 甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )
甲、乙两名滑冰运动员,M甲=60kg,M乙=40kg,面对面拉着弹簧称做匀速圆周运动的滑冰表演,如图所示,两人相距2m,弹簧称的示数为192N,下列判断中正确的是( )| A. | 两人的线速度相同,为2m/s | |
| B. | 两人的角速度相同,为2rad/s | |
| C. | 两人的运动半径相同,都是1m | |
| D. | 两人的运动半径不同,甲为0.8m,乙为1.2m |
4. 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
 如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )
如图所示为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图,波速为3m/s,则下列说法中正确的是( )| A. | 质点P此时可的振动方向沿y轴负方向 | |
| B. | 质点P的振幅比质点Q的振幅小 | |
| C. | 波的频率为0.25Hz | |
| D. | 质点P,Q的平衡位置间距离为6.5m | |
| E. | 从图示时刻开始,再经$\frac{7}{12}$s,质点P,Q的位移第一次相等 |
 如图所示,单匝矩形线圈在匀强磁场中绕垂直于磁场方向的中心轴匀速转动,线圈总电阻r=2Ω,转动周期为0.02s,产生的感应电动势的最大值为Em=20V,线圈通过电刷与一个阻值为R=8Ω的电阻相连.
如图所示,单匝矩形线圈在匀强磁场中绕垂直于磁场方向的中心轴匀速转动,线圈总电阻r=2Ω,转动周期为0.02s,产生的感应电动势的最大值为Em=20V,线圈通过电刷与一个阻值为R=8Ω的电阻相连.
 如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少?
如图所示,水平传送带以速度v匀速运动,一质量为m的小木块由静止轻放到传送带上,若小木块与传送带之间的动摩擦因数为μ,当小木块与传送带相对静止时,转化为内能的能量是多少? 如图所示,长度l=3m、倾角θ=37°的光滑斜面固定在水平面上,小球p从斜面顶端A点静止滑下时,小球q也从A点正上方的D点水平抛出,两球同时到达斜面底端的B点.不计空气阻力,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,长度l=3m、倾角θ=37°的光滑斜面固定在水平面上,小球p从斜面顶端A点静止滑下时,小球q也从A点正上方的D点水平抛出,两球同时到达斜面底端的B点.不计空气阻力,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求: