题目内容
7.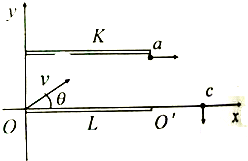 如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:
如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:(1)K极板所带电荷的电性;
(2)粒子经过c点时速度大小
(3)圆形磁场区域的最小面积
(4)粒子从O到c所经历的时间.
分析 (1)根据左手定则和运动轨迹即可判断
(2)带电粒子在电容器中做匀变速曲线运动,在磁场中做匀速圆周运动,画出运动轨迹,把速度分解到沿x轴方向和沿y轴方向,根据几何关系求出到达a点的速度;
(3)粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力,求出圆周运动的半径,再根据几何关系求出ac的长度,ac即为圆形磁场的最小直径,根据圆的面积公式求出最小面积.
(4)粒子从O到a,在y轴方向上做匀减速直线运动,根据牛顿第二定律求解加速度,根据速度的分解求出沿y轴的初速度,进而求出运动的时间,粒子从a到c的过程中,运动的时间为$\frac{1}{4}$T,两段时间之和即为所求时间.
解答 解:(1)在磁场中,由左手定则可知粒子带正电,由粒子在电容器间运动时,向L极板偏转,所以K板带正电
(2)带电粒子在电容器中做匀变速曲线运动,在磁场中做匀速圆周运动,轨迹如图所示: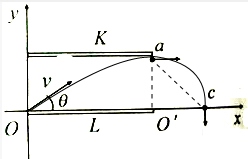
粒子在x轴方向做匀速直线运动,在y轴方向做匀减速直线运动,经过K板边缘a点平行于x轴飞出电容器,
则粒子在x轴上的分量为 va=vcosθ=$\sqrt{3}$$\frac{E}{B}$•$\frac{\sqrt{3}}{3}$=$\frac{E}{B}$,粒子在磁场中做匀速圆周运动,则到达c点时速度大小为 vc=$\frac{E}{B}$.
(2)粒子从c点垂直穿过x轴离开磁场,又已知∠acO=45°,所以粒子在磁场中运动轨迹为$\frac{1}{4}$圆弧
则圆形磁场直径最小为ac的长度,根据几何关系得:
ac=$\sqrt{2}$
粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有:
Bqv=m$\frac{{v}^{2}}{R}$,解得:R=$\frac{m{v}_{c}}{qB}$=$\frac{mE}{{B}^{2}q}$
所以 ac=$\frac{\sqrt{2}mE}{{B}^{2}q}$
则圆形磁场区域的最小面积S=($\frac{ac}{2}$)2π=$\frac{π{m}^{2}{E}^{2}}{2{B}^{4}{q}^{2}}$
(4)粒子从O到a,在y轴方向上做匀减速直线运动,加速度大小 a=$\frac{qE}{m}$
则粒子从O到a运动的时间 t1=$\frac{vsinθ}{a}$=$\frac{\sqrt{2}m}{Bq}$
粒子从a到c的过程中,运动的时间为 t2=$\frac{1}{4}$T=$\frac{1}{4}$×$\frac{2πm}{Bq}$=$\frac{πm}{2Bq}$
则粒子从O到c所经历的时间t=t1+t2=$\frac{(2\sqrt{2}+π)m}{2Bq}$
答:(1)K极板所带电荷的电性是正电;
(2)粒子经过c点时速度大小为$\frac{E}{B}$.
(3)圆形磁场区域的最小面积是$\frac{π{m}^{2}{E}^{2}}{2{B}^{4}{q}^{2}}$.
(4)粒子从O到c所经历的时间为$\frac{(2\sqrt{2}+π)m}{2Bq}$.
点评 本题是一道力学综合题,考查了粒子在电场、磁场中的运动,分析清楚粒子运动过程是正确解题的关键,分析清楚运动过程后,应用牛顿第二定律、运动学公式即可正确解题.

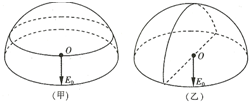 一半径为R的半球面均匀带有正电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{kQ}{2{R}^{2}}$,方向如图所示.把半球面分为表面积相等的上、下两部分,如图甲所示,上、下两部分电荷在球心O处产生电场的场强大小分别为E1、E2;把半球面分为表面积相等的左、右两部分,如图乙所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E3、E4.则( )
一半径为R的半球面均匀带有正电荷Q,电荷Q在球心O处产生的场强大小E0=$\frac{kQ}{2{R}^{2}}$,方向如图所示.把半球面分为表面积相等的上、下两部分,如图甲所示,上、下两部分电荷在球心O处产生电场的场强大小分别为E1、E2;把半球面分为表面积相等的左、右两部分,如图乙所示,左、右两部分电荷在球心O处产生电场的场强大小分别为E3、E4.则( )| A. | E1<$\frac{kQ}{4{R}^{2}}$ | B. | E2=$\frac{kQ}{4{R}^{2}}$ | C. | E3>$\frac{kQ}{4{R}^{2}}$ | D. | E4=$\frac{kQ}{4{R}^{2}}$ |
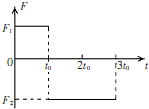 一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )
一静止的物体所受到的合外力随时间的变化关系如图所示,图中F1、F2未知.已知物体从t=0时刻出发,在3t0时刻恰又返回到出发点,则( )| A. | O~to物体做匀加速直线运动,to-3to物体做匀减速直线运动 | |
| B. | 物体在F1作用下的位移与在F2作用下的位移相等 | |
| C. | t0时刻物体的速度与3t0时刻物体的速度大小之比为$\frac{2}{3}$ | |
| D. | F1与F2大小之比为$\frac{6}{5}$ |
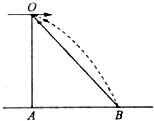 如图所示,在平台末端与水平面之间有一光滑斜杆,现有两个相同的金属小环,M环从平台末端O点水平抛出,同时N环穿过斜杆从顶端由静止释放,如果抛出的金属环恰能落在斜杆末端的B点,则关于这两个金属环的运动,不计空气阻力,下列说法正确的是( )
如图所示,在平台末端与水平面之间有一光滑斜杆,现有两个相同的金属小环,M环从平台末端O点水平抛出,同时N环穿过斜杆从顶端由静止释放,如果抛出的金属环恰能落在斜杆末端的B点,则关于这两个金属环的运动,不计空气阻力,下列说法正确的是( )| A. | 两环同时到达B点 | |
| B. | M环先到达B点 | |
| C. | AB距离越大,两环到达B点的时间差越大 | |
| D. | 两环运动过程中处于同一高度时重力的瞬时功率相同 |
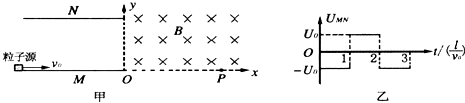
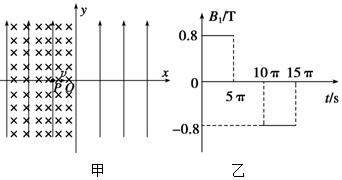
 地磁场会对精密仪器中的显像管产生影响.在电子显像管内部,由炽热的灯丝上发射出的电子(可视为初速度为0),在经过电压为U的电场加速后,在不加偏转电场、磁场时,电子(质量为m、电荷量为e,不计重力)应沿直线运动打在荧光屏的正中心位置O.在南极,科考队设备中的显像管由于地磁场的影响,在未加偏转磁场时电子束也会偏离直线运动.设显像管水平放置,地磁场磁感强度的方向竖直向上,大小为B(俯视图如图所示),忽略地磁场对电子在加速过程中的影响,加速电场边缘到荧光屏的距离为l.求在地磁场的影响下:
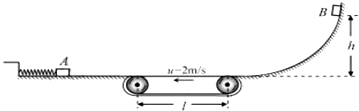
地磁场会对精密仪器中的显像管产生影响.在电子显像管内部,由炽热的灯丝上发射出的电子(可视为初速度为0),在经过电压为U的电场加速后,在不加偏转电场、磁场时,电子(质量为m、电荷量为e,不计重力)应沿直线运动打在荧光屏的正中心位置O.在南极,科考队设备中的显像管由于地磁场的影响,在未加偏转磁场时电子束也会偏离直线运动.设显像管水平放置,地磁场磁感强度的方向竖直向上,大小为B(俯视图如图所示),忽略地磁场对电子在加速过程中的影响,加速电场边缘到荧光屏的距离为l.求在地磁场的影响下: 如图所示为电影《星际穿越》中飞船图片,为了模拟重力环境,可以让飞船旋转起来.对飞行的飞船用Tracker Video Analysis 软件进行分析,得出飞船角速度为0.6rad/s,已知地球表面重力加速度为10m/s2,由此推算出飞船的半径约为( )
如图所示为电影《星际穿越》中飞船图片,为了模拟重力环境,可以让飞船旋转起来.对飞行的飞船用Tracker Video Analysis 软件进行分析,得出飞船角速度为0.6rad/s,已知地球表面重力加速度为10m/s2,由此推算出飞船的半径约为( )