题目内容
19. 地磁场会对精密仪器中的显像管产生影响.在电子显像管内部,由炽热的灯丝上发射出的电子(可视为初速度为0),在经过电压为U的电场加速后,在不加偏转电场、磁场时,电子(质量为m、电荷量为e,不计重力)应沿直线运动打在荧光屏的正中心位置O.在南极,科考队设备中的显像管由于地磁场的影响,在未加偏转磁场时电子束也会偏离直线运动.设显像管水平放置,地磁场磁感强度的方向竖直向上,大小为B(俯视图如图所示),忽略地磁场对电子在加速过程中的影响,加速电场边缘到荧光屏的距离为l.求在地磁场的影响下:
地磁场会对精密仪器中的显像管产生影响.在电子显像管内部,由炽热的灯丝上发射出的电子(可视为初速度为0),在经过电压为U的电场加速后,在不加偏转电场、磁场时,电子(质量为m、电荷量为e,不计重力)应沿直线运动打在荧光屏的正中心位置O.在南极,科考队设备中的显像管由于地磁场的影响,在未加偏转磁场时电子束也会偏离直线运动.设显像管水平放置,地磁场磁感强度的方向竖直向上,大小为B(俯视图如图所示),忽略地磁场对电子在加速过程中的影响,加速电场边缘到荧光屏的距离为l.求在地磁场的影响下:(1)电子在偏转时的加速度的大小;
(2)电子在荧光屏上偏移的距离.
分析 (1)先对直线加速过程根据动能定理列式求解末速度;对偏转过程,根据牛顿第二定律列式求解加速度;
(2)电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律列式求解轨道半径,结合几何关系确定电子在荧光屏上偏移的距离.
解答  解:(1)设从加速电场射出的电子速度为v0,则根据动能定理有:
解:(1)设从加速电场射出的电子速度为v0,则根据动能定理有:
$\frac{1}{2}m{v_0}^2=eU$
从加速电场射出的电子在地磁场中受到洛伦兹力的作用而做匀速圆周运动,设电子的加速度为a,则:
ev0B=ma
由以上各式解得:
$a=\frac{eB}{m}\sqrt{\frac{2eU}{m}}$
(2)设电子在地磁场中运动的半径为R,
根据牛顿第二定律:
$e{v_0}B=m\frac{v_0^2}{R}$
解得:
$R=\frac{{m{v_0}}}{eB}$
设电子在荧光屏上偏移的距离为x,
根据图中的几何关系,有:
$x=R-\sqrt{{R^2}-{l^2}}$
结合以上关系,得:
$x=\frac{1}{B}\sqrt{\frac{2mU}{e}}-\sqrt{\frac{2mU}{{e{B^2}}}-{l^2}}$
答:(1)电子在偏转时的加速度的大小为$\frac{eB}{m}\sqrt{\frac{2eU}{m}}$;
(2)电子在荧光屏上偏移的距离为$\frac{1}{B}\sqrt{\frac{2mU}{e}}-\sqrt{\frac{2mU}{e{B}^{2}}-{l}^{2}}$.
点评 电子先直线加速、再做匀速圆周运动,对直线加速过程根据动能定理列式,对匀速圆周运动根据牛顿第二定律列式,关键是画出运动轨迹,结合几何关系分析.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
9.如图所示,实线和虚线分别表示某电场的电场线和等势线,下列说法中正确的是( )

| A. | c点场强大于a点场强 | |
| B. | c点电势高于a点电势 | |
| C. | c、b两点间的电势差大于c、a两点间的电势差 | |
| D. | 若将一试探电荷+q由a点移动到b点,电场力做正功 |
14. 如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
 如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )| A. | $\frac{0.3π}{{G{T^2}}}$ | B. | $\frac{3π}{{G{T^2}}}$ | C. | $\frac{10π}{{3G{T^2}}}$ | D. | $\frac{30π}{{G{T^2}}}$ |
4.图甲所示为氢原子的能级,图乙为氢原子的光谱.已知谱线a是氢原子从n=4的能级跃迁到n=2能级时的辐射光,则谱线b可能是氢原子( )时的辐射光


| A. | 从n=5的能级跃迁到n=3的能级 | B. | 从n=4的能级跃迁到n=3的能级 | ||
| C. | 从n=5的能级跃迁到n=2的能级 | D. | 从n=3的能级跃迁到n=2的能级 |
11. 一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
 一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )| A. | △EJ2=2△EJ1,△EP2=2△EP1 | B. | △EJ2>2△EJ1,△EP2>2△EP1 | ||
| C. | △EJ2=4△EJ1,△EP2<△EP1 | D. | △EJ2<4△EJ1,△EP2=2△EP1 |
8.质量为m的物体,沿光滑斜面开始下滑,斜面的倾角为θ,当它在竖直方向上下降h高度时的重力的即时功率为( )
| A. | mg$\sqrt{2gh}$ | B. | mg$\sqrt{2gh}$cosθ | C. | mg$\sqrt{2ghsinθ}$ | D. | mg$\sqrt{2gh}$sinθ |
 一气缸质量为M=60kg(气缸的厚度忽略不计且透热性良好),开口向上放在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞质量m=10kg.气缸内封闭了一定质量的理想气体,此时气柱长度为L1=0.4m.已知大气压为po=1×105Pa.现用力缓慢向上拉动活塞,若使气缸能离开地面,气缸的高度至少是多少?(取重力加速度g=l0m/s2.)
一气缸质量为M=60kg(气缸的厚度忽略不计且透热性良好),开口向上放在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞质量m=10kg.气缸内封闭了一定质量的理想气体,此时气柱长度为L1=0.4m.已知大气压为po=1×105Pa.现用力缓慢向上拉动活塞,若使气缸能离开地面,气缸的高度至少是多少?(取重力加速度g=l0m/s2.)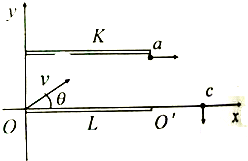 如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:
如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求: 如图所示,竖直放置的金属薄板M、N间距为d.绝缘水平直杆左端从N板中央的小孔穿过,与M板固接,右端处在磁感应强度为B的匀强磁场中.质量为m、带电量为+q的中空小球P,套在水平直杆上,紧靠M板放置,与杆的动摩擦因数为μ.当在M、N板间加上适当的电压U后,P球将沿水平直杆从N板小孔射出,试问:
如图所示,竖直放置的金属薄板M、N间距为d.绝缘水平直杆左端从N板中央的小孔穿过,与M板固接,右端处在磁感应强度为B的匀强磁场中.质量为m、带电量为+q的中空小球P,套在水平直杆上,紧靠M板放置,与杆的动摩擦因数为μ.当在M、N板间加上适当的电压U后,P球将沿水平直杆从N板小孔射出,试问: