题目内容
12.如图甲所示,在xOy平面内有足够大的匀强电场.电场方向竖直向上,电场强度E=40N/C,在y轴左侧平面内有足够大的磁场,磁感应强度B1随时间t变化的规律如图乙所示,15π s后磁场消失,选定磁场垂直纸面向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8T,t=0时刻,一质量m=8×10-4kg、电荷量q=+2×10-4C的微粒从x轴上xp=-0.8m处的P点以速度v=0.12m/s 向x轴正方向入射.(g取10m/s2)(1)求微粒在第二象限运动过程中离x轴、y轴的最大距离.
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x,y).
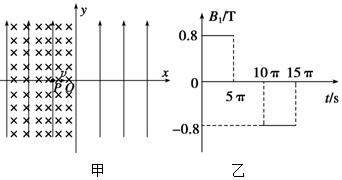
分析 (1)根据电场力等于重力,则洛伦兹力提供向心力,做匀速圆周运动,得出半径与周期公式.并根据几何关系与运动学公式的位移,即可求解;
(2)根据粒子做匀速圆周运动,求出半径.从而得出与已知长度的函数关系,最终求出M点的坐标;
解答 解:(1)因为微粒射入电磁场后受到的电场力和重力分别为:
F电=Eq=8×10-3 N,G=mg=8×10-3 N
F电=G,所以微粒在洛伦兹力作用下做匀速圆周运动,由牛顿第二定律有:
$qv{B}_{1}=m\frac{{v}^{2}}{{R}_{1}}$
所以R1=$\frac{mv}{{B}_{1}q}$=0.6 m
T=$\frac{2πm}{{B}_{1}q}$=10π s
从图乙可知在0~5 π s内微粒向左做匀速圆周运动,在5π s~10π s内微粒向左匀速运动,运动位移为:
x1=v$\frac{T}{2}$=0.6π m
在10π s~15π s内,微粒又做匀速圆周运动,15π s以后向右匀速运动,之后穿过y轴.所以,离y轴的最大距离为:
s=0.8 m+x1+R1=1.4 m+0.6π m≈3.3 m
离x轴的最大距离s′=2R1×2=4R1=2.4 m
(2)如图,微粒穿过圆形磁场要求偏转角最大,入射点A与出射点B的连线必须为磁场圆的直径 ,由牛顿第二定律,有:
,由牛顿第二定律,有:
qvB2=$\frac{m{v}_{2}}{{R}_{2}}$
所以R2=$\frac{mv}{{B}_{2}q}$=0.6 m=2r
所以最大偏转角为:θ=60°
所以圆心坐标为:x=0.30 m
y=s-rcos 60°=2.4 m-0.3 m×$\frac{1}{2}$=2.25 m,
即磁场的圆心坐标为(0.30,2.25)
答:(1)微粒在第二像限运动过程中离y轴的最大距离3.2m;离开x轴的最大距离2.4m;
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(0.3m、2.25m)
点评 本题是力学与电学综合题,根据匀速圆周运动的规律与几何关系相结合,同时运用力学与电学的知识来解题,从而培养学生分析问题的方法,提升解题的能力.

 名校课堂系列答案
名校课堂系列答案
| A. | 从n=5的能级跃迁到n=3的能级 | B. | 从n=4的能级跃迁到n=3的能级 | ||
| C. | 从n=5的能级跃迁到n=2的能级 | D. | 从n=3的能级跃迁到n=2的能级 |
 理想变压器原线圈接电压为u=U0sinωt的交流电源上,在变压器次级线圈中分别安装有甲、乙两插座,导线电阻为R,电路如图所示.插座不接用电器时小灯泡正常发光,将某一用电器接在甲或乙插座上,下列说法正确的是( )
理想变压器原线圈接电压为u=U0sinωt的交流电源上,在变压器次级线圈中分别安装有甲、乙两插座,导线电阻为R,电路如图所示.插座不接用电器时小灯泡正常发光,将某一用电器接在甲或乙插座上,下列说法正确的是( )| A. | 若接在甲上,电压表示数不变,灯变暗 | |
| B. | 若接在甲上,电压表示数不变,灯变亮 | |
| C. | 若接在乙上,电压表示数变大,灯变亮 | |
| D. | 若接在乙上,电压表示数变小,灯变暗 |
 如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )
如图所示,光滑水平面上有一矩形长木板,木板左端放一小物块,已知木板质量大于物块质量,t=0时两者从图中位置以相同的水平速度v0向右运动,碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来,运动过程中物块一直未离开木板,则关于物块运动的速度v随时间t变化的图象可能正确的是( )




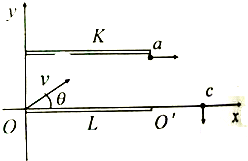 如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:
如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:
