题目内容
2.如图所示,装置的左边是足够长的光滑水平面,一轻质弹簧左端固定,右端连接着质量 M=2kg的小物块A.装置的中间是水平传送带,它与左右两边的台面等高,并能平滑对接.传送带始终以u=2m/s的速率逆时针转动.装置的右边是一光滑的曲面,质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放.已知物块B与传送带之间的摩擦因数μ=0.2,l=1.0m.设物块A、B中间发生的是对心弹性碰撞,第一次碰撞前物块A静止且处于平衡状态.取g=10m/s2.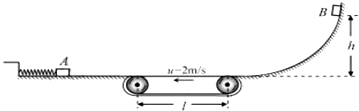
(1)求物块B与物块A第一次碰撞前速度大小;
(2)通过计算说明物块B与物块A第一次碰撞后能否运动到右边曲面上?
分析 (1)物块B沿光滑曲面下滑到水平位置由机械能守恒列出等式,物块B在传送带上滑动根据牛顿第二定律和运动学公式求解
(2)物块A、B第一次碰撞前后运用动量守恒,能量守恒列出等式求解
解答 解:(1)设物块B沿光滑曲面下滑到水平位置时的速度大小为v0,由机械能守恒知
$mgh=\frac{1}{2}m{{v}_{0}}^{2}$ ①
设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a
μmg=ma ②
设物块B通过传送带后运动速度大小为v,有${v}^{2}-{{v}_{0}}^{2}=-2al$ ③
结合②③④式解得 v=4m/s ④
由于v>u=2m/s,所以v=4m/s即为物块B与A第一次碰撞前的速度大小.
(2)设物块B、A第一次弹性碰撞后的速度分别为v1、v2,取向右为正方向
-mv=mv1+Mv2 ⑤
$\frac{1}{2}m{v}^{2}=\frac{1}{2}m{{v}_{1}}^{2}+\frac{1}{2}M{{v}_{2}}^{2}$ ⑥
解得:${v}_{1}=\frac{1}{3}v=\frac{4}{3}m/s$ ⑦
即碰撞后B沿水平台面向右匀速运动
设物块B在传送带上向右运动的最大位移为l′,则
$0-{{v}_{1}}^{2}=-2al′$ ⑧
解得$l′=\frac{4}{9}m<1m$ ⑨
所以物块B不能通过传送带运动到右边的曲面上.
答:(1)物块B与物块A第一次碰撞前速度大小为4m/s;
(2)物块B不能通过传送带运动到右边的曲面上.
点评 本题是多过程问题,分析滑块经历的过程,运用动量守恒,能量守恒、牛顿第二定律和运动学公式结合按时间顺序分析和计算,难度较大.

练习册系列答案
相关题目
13.如图甲为理想变压器的示意图,其原、副线圈的匝数比为4:1,电压表和电流表均为理想电表,R1为阻值随温度升高而变小的热敏电阻,R1为定值电阻.若发电机向原线圈输入如图乙所示的正弦交流电.下列说法中正确的是( )


| A. | 输入变压器原线圈的交流电压的表达式为u=36$\sqrt{2}$sin50πtV | |
| B. | 变压器原、副线圈中的电流之比为4:1 | |
| C. | t=0.01s时,发电机的线圈平面位于中性面 | |
| D. | R1温度升高时,变压器的输入功率变小 |
17. 如图所示是静电除尘的原理示意图,A为金属管,B为金属丝,在A、B之间接上高电压,使B附近的空气分子被强电场电离为电子和正离子,电子在向A极运动过程中被烟气中的煤粉俘获,使煤粉带负电,最终被吸附到A极上,排出的烟就比较清洁了.有关静电除尘的装置,下列说法正确的是( )
如图所示是静电除尘的原理示意图,A为金属管,B为金属丝,在A、B之间接上高电压,使B附近的空气分子被强电场电离为电子和正离子,电子在向A极运动过程中被烟气中的煤粉俘获,使煤粉带负电,最终被吸附到A极上,排出的烟就比较清洁了.有关静电除尘的装置,下列说法正确的是( )
 如图所示是静电除尘的原理示意图,A为金属管,B为金属丝,在A、B之间接上高电压,使B附近的空气分子被强电场电离为电子和正离子,电子在向A极运动过程中被烟气中的煤粉俘获,使煤粉带负电,最终被吸附到A极上,排出的烟就比较清洁了.有关静电除尘的装置,下列说法正确的是( )
如图所示是静电除尘的原理示意图,A为金属管,B为金属丝,在A、B之间接上高电压,使B附近的空气分子被强电场电离为电子和正离子,电子在向A极运动过程中被烟气中的煤粉俘获,使煤粉带负电,最终被吸附到A极上,排出的烟就比较清洁了.有关静电除尘的装置,下列说法正确的是( )| A. | 金属管内形成的电场为匀强电场 | |
| B. | D为烟气的进气口,C为排气口 | |
| C. | 金属管A应接高压电源的正极,金属丝B接负极 | |
| D. | 以上说法均不正确 |
14. 如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
 如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )
如图所示,一个质量均匀分布的星球,绕其中心轴PQ自转,AB与PQ是互相垂直的直径.星球在A点的重力加速度是P点的90%,星球自转的周期为 T,万有引力常量为G,则星球的密度为( )| A. | $\frac{0.3π}{{G{T^2}}}$ | B. | $\frac{3π}{{G{T^2}}}$ | C. | $\frac{10π}{{3G{T^2}}}$ | D. | $\frac{30π}{{G{T^2}}}$ |
11. 一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
 一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )
一物体静止在粗糙斜面上,现用一大小为F1的水平拉力拉动物体,经过时间t后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过时间t后速度变为2v,对于上述两个过程.用△EJ1,△EJ2分别表示前后两次物体增加的机械能,△EP1,△EP2分别表示前后两次物体增加的重力势能,则( )| A. | △EJ2=2△EJ1,△EP2=2△EP1 | B. | △EJ2>2△EJ1,△EP2>2△EP1 | ||
| C. | △EJ2=4△EJ1,△EP2<△EP1 | D. | △EJ2<4△EJ1,△EP2=2△EP1 |
 如图所示,均匀薄壁U型管竖直放置,左管竖直部分高度大于30cm且上端封闭,右管上端开口且足够长,用两段水银封闭了A、B两部分理想气体,下方水银左右液面等高,右管上方的水银柱高h=4cm,初状态温度为27℃,A气体长度l1=15cm,大气压强p0=76cmHg.现使整个装置缓慢升温,当下方水银的左右液面高度相差△l=10cm时,保持温度不变,再向右管中缓慢注入水银,使A中气柱长度回到15cm.求:
如图所示,均匀薄壁U型管竖直放置,左管竖直部分高度大于30cm且上端封闭,右管上端开口且足够长,用两段水银封闭了A、B两部分理想气体,下方水银左右液面等高,右管上方的水银柱高h=4cm,初状态温度为27℃,A气体长度l1=15cm,大气压强p0=76cmHg.现使整个装置缓慢升温,当下方水银的左右液面高度相差△l=10cm时,保持温度不变,再向右管中缓慢注入水银,使A中气柱长度回到15cm.求: 一气缸质量为M=60kg(气缸的厚度忽略不计且透热性良好),开口向上放在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞质量m=10kg.气缸内封闭了一定质量的理想气体,此时气柱长度为L1=0.4m.已知大气压为po=1×105Pa.现用力缓慢向上拉动活塞,若使气缸能离开地面,气缸的高度至少是多少?(取重力加速度g=l0m/s2.)
一气缸质量为M=60kg(气缸的厚度忽略不计且透热性良好),开口向上放在水平面上,气缸中有横截面积为S=100cm2的光滑活塞,活塞质量m=10kg.气缸内封闭了一定质量的理想气体,此时气柱长度为L1=0.4m.已知大气压为po=1×105Pa.现用力缓慢向上拉动活塞,若使气缸能离开地面,气缸的高度至少是多少?(取重力加速度g=l0m/s2.)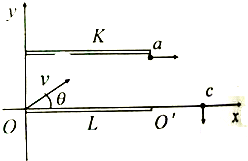 如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求:
如图所示,有一平行板电容器左边缘在y轴上,下极板与x轴重合,极板间匀强电场的场强为E,一电量为q,质量为m的带电粒子.速度大小为$\sqrt{3}$$\frac{E}{B}$,从O点与x轴成θ角斜向上射入极板间,粒子经过K板边缘a点平行于x轴飞出电容器,立即进入一磁感应强度为B的圆形磁场(图中未画),随后从c点垂直穿过x轴离开磁场.已知∠aco=45°,cosθ=$\frac{\sqrt{3}}{3}$,磁场方向垂直于坐标平面向外,且磁场与电容器不重合,带电粒子重力不计,试求: