题目内容
4. 两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L,导轨上面横放着两根导体棒ab和cd,构成矩形回路,如图所示.两根导体棒的质量均为m,棒ab和cd的有效电阻分别为R和2R.回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B.设两导体棒均可沿导轨无摩擦地滑行,开始时,棒cd静止,棒ab有指向棒cd的初速度v0,若两导体棒在运动中始终不接触,求:
两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L,导轨上面横放着两根导体棒ab和cd,构成矩形回路,如图所示.两根导体棒的质量均为m,棒ab和cd的有效电阻分别为R和2R.回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B.设两导体棒均可沿导轨无摩擦地滑行,开始时,棒cd静止,棒ab有指向棒cd的初速度v0,若两导体棒在运动中始终不接触,求:(1)在运动过程棒ab产生的焦耳热最多是多少?
(2)当ab棒的速度变为初速度的$\frac{4}{5}$时,棒cd的速度和加速度分别是多少?
分析 (1)由动量守恒定律求解共同速度,根据能的转化和守恒定律和能量分配关系求解ab产生的焦耳热;
(2)根据动量守恒定律求解棒cd的速度,根据牛顿第二定律求解加速度.
解答 解:(1)当两棒速度相等时系统产生的焦耳热最多;在运动过程中两棒总动量守恒,取向右为正方向,由动量守恒定律得:mυ0=2mυ
得共同速度为:υ=$\frac{1}{2}$υ0
根据能的转化和守恒定律得:Q=$\frac{1}{2}$mυ02-$\frac{1}{2}$•2mυ2=$\frac{1}{4}$mυ02.
所以在运动过程棒ab产生的焦耳热最多是为:QR=$\frac{R}{R+2R}Q$=$\frac{1}{12}$mυ02;
(2)当ab棒的速度变为初速度的$\frac{4}{5}$时,即v1=$\frac{4}{5}{v}_{0}$,设cd棒的速度为v2,根据动量守恒定律可得:mυ0=mv1+mv2
解得:v2=$\frac{1}{5}{v}_{0}$;
根据法拉第电磁感应定律可得感应电动势为:E=BL(v1-v2)=$\frac{3}{5}{BLv}_{0}$,
根据闭合电路的欧姆定律可得感应电流为:I=$\frac{E}{3R}=\frac{BL{v}_{0}}{5R}$,
根据牛顿第二定律可得棒cd的加速度为:a=$\frac{BIL}{m}$=$\frac{{B}^{2}{L}^{2}{v}_{0}}{5mR}$.
答:(1)在运动过程棒ab产生的焦耳热最多是$\frac{1}{12}$mυ02;
(2)当ab棒的速度变为初速度的$\frac{4}{5}$时,棒cd的速度为$\frac{1}{5}{v}_{0}$,加速度是$\frac{{B}^{2}{L}^{2}{v}_{0}}{5mR}$.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的平衡问题,根据平衡条件列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.

 如图所示,某运动员拖着旧橡胶轮胎进行耐力训练,轮胎始终未脱离地面,分析其在水平直道上跑100m的过程中,下列说法正确的是( )
如图所示,某运动员拖着旧橡胶轮胎进行耐力训练,轮胎始终未脱离地面,分析其在水平直道上跑100m的过程中,下列说法正确的是( )| A. | 轮胎受到的重力对轮胎做了正功 | |
| B. | 轮胎受到地面的摩擦力对轮胎做了负功 | |
| C. | 轮胎受到的拉力对轮胎不做功 | |
| D. | 轮胎受到地面的支持力对轮胎做了正功 |
 如图,同一水平面上放置的两根光滑金属导轨POQ与P′O′Q′,完全相同,电阻不计,处于相互平行的竖直平面内,间距为L,轨道顶角为直角,左侧轨道倾角为θ,匀强磁场垂直于左侧轨道平面上,磁感应强度大小为B,两根相同的金属棒ab,cd,质量为m,电阻为r,分别从导轨左右两侧某位置由静止释放,在以后的过程中,ab,cd始终与导轨保持垂直且接触良好.(两侧轨道足够长),则( )
如图,同一水平面上放置的两根光滑金属导轨POQ与P′O′Q′,完全相同,电阻不计,处于相互平行的竖直平面内,间距为L,轨道顶角为直角,左侧轨道倾角为θ,匀强磁场垂直于左侧轨道平面上,磁感应强度大小为B,两根相同的金属棒ab,cd,质量为m,电阻为r,分别从导轨左右两侧某位置由静止释放,在以后的过程中,ab,cd始终与导轨保持垂直且接触良好.(两侧轨道足够长),则( )| A. | ab棒最大速度v=$\frac{2mgrsinθ}{{B}^{2}{L}^{2}}$ | |
| B. | ab棒减少的重力势能等于整个回路的焦耳热 | |
| C. | cd棒不受安培力作用 | |
| D. | cd棒机械能守恒 |
| A. | 不同频率的声波在同一均匀介质中的传播速度均相等 | |
| B. | 利用单摆测重力加速度实验中,小球的质量不需要测量 | |
| C. | 受迫振动物体的频率等于物体的固有频率,与驱动力频率无关 | |
| D. | 技术人员用超声波探测金属、陶瓷、混凝土中是否有气泡是利用了多普勒效应 | |
| E. | 潜艇利用声呐探测周围物体的分布情况,用的是波的反射原理 |
 如图所示,长木板A放在光滑的水平面上,物体B以水平速度v0冲上A后,由于摩擦力作用,最后停止在木板A上,则从B冲上木板知道两者相对于静止的过程中,下列说法正确的是( )
如图所示,长木板A放在光滑的水平面上,物体B以水平速度v0冲上A后,由于摩擦力作用,最后停止在木板A上,则从B冲上木板知道两者相对于静止的过程中,下列说法正确的是( )| A. | 物体B动能的减少量等于B克服摩擦力做的功 | |
| B. | 物体B的动量变化量与物体A的动量变化量相同 | |
| C. | 物体B损失的动能等于木板A获得的动能 | |
| D. | AB组成系统机械能的损失量等于系统内能的增量 |
| A. | 该船可能垂直河岸横渡到对岸 | |
| B. | 当船头垂直河岸横渡时,过河所用的时间最10s | |
| C. | 当船头垂直河岸横渡时,船的位移最小是100m | |
| D. | 该船船头无论朝向哪个方向渡到对岸,船到对岸的位移都大于100m |
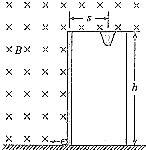 如图所示,水平地面上方有绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-5C,可视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况),g=10m/s2,求:
如图所示,水平地面上方有绝缘弹性竖直挡板,板高h=9m,与板等高处有一水平放置的篮筐,筐口的中心离挡板s=3m.板的左侧以及上端与筐口的连线上方存在匀强磁场和匀强电场,磁场方向垂直纸面向里,磁感应强度B=1T;质量m=1×10-3kg、电荷量q=-1×10-5C,可视为质点的带电小球从挡板最下端,以某一速度水平射入场中做匀速圆周运动,若与挡板相碰就以原速率弹回,且碰撞时间不计,碰撞时电荷量不变,小球最后都能从筐口的中心处落入筐中(不考虑与地面碰撞后反弹入筐情况),g=10m/s2,求: 如图所示,倾角为θ的足够长的平行导轨固定在水平面上,两根完全相同的导体棒M、N垂直导轨放置,导体棒的长度与导轨之间的距离相等,开始时两导体棒静止在导轨上,整个装置置于垂直导轨平面向上、磁感应强度为B的匀强磁场中.已知每根导体棒的质量均为m、长度均为d、阻值均为r,导轨的电阻忽略不计,两导体棒与导轨之间的动摩擦因数均为μ=tanθ.现给导体棒M一沿导轨平面向下的初速度v0,整个过程两导体棒始终与导轨保持良好的接触.求:
如图所示,倾角为θ的足够长的平行导轨固定在水平面上,两根完全相同的导体棒M、N垂直导轨放置,导体棒的长度与导轨之间的距离相等,开始时两导体棒静止在导轨上,整个装置置于垂直导轨平面向上、磁感应强度为B的匀强磁场中.已知每根导体棒的质量均为m、长度均为d、阻值均为r,导轨的电阻忽略不计,两导体棒与导轨之间的动摩擦因数均为μ=tanθ.现给导体棒M一沿导轨平面向下的初速度v0,整个过程两导体棒始终与导轨保持良好的接触.求: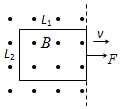 如图所示,长L1、宽L2、电阻为R的单匝矩形线圈放置在光滑绝缘的水平桌面上,匀强磁场的磁感应强度为B、方向竖直向上,线圈的右边框正好处于匀强磁场的边缘,线圈平面与磁感线垂直.现施加一水平向右的拉力使线圈以速度v匀速向右运动.
如图所示,长L1、宽L2、电阻为R的单匝矩形线圈放置在光滑绝缘的水平桌面上,匀强磁场的磁感应强度为B、方向竖直向上,线圈的右边框正好处于匀强磁场的边缘,线圈平面与磁感线垂直.现施加一水平向右的拉力使线圈以速度v匀速向右运动.