题目内容
7. 一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m 处下潜到深度为h2=4.0m 时,看到标记刚好被浮标挡住,此处看不到船尾端 Q;继续下△h=4.0m,恰好能看见Q.求:
一赛艇停在平静的水面上,赛艇前端有一标记P离水面的高度为h1=0.6m,尾部下端Q略高于水面;赛艇正前方离赛艇前端s1=0.8m处有一浮标,示意如图.一潜水员在浮标前方s2=3.0m 处下潜到深度为h2=4.0m 时,看到标记刚好被浮标挡住,此处看不到船尾端 Q;继续下△h=4.0m,恰好能看见Q.求:(i)水的折射率n;
(ii)赛艇的长度l.(可用根式表示)
分析 (1)由题意可作出光路图,由几何关系可知入射角和折射角,则可求得折射率;
(2)由题意可知潜水员和Q点的连线与竖直方向夹角刚好为临界角,由几何知识可解得赛艇的长度.
解答 解:(1)设过P点光线,恰好被浮子挡住时,入射角、折射角分别为α、β,则:
sinα=$\frac{{s}_{1}}{\sqrt{{s}_{1}^{2}+{h}_{1}^{2}}}$ ①
sinβ=$\frac{{s}_{2}}{\sqrt{{s}_{2}^{2}+{h}_{2}^{2}}}$ ②
则水的折射率为 n=$\frac{sinα}{sinβ}$ ③
由①②③联立,代入数据解得:n=$\frac{4}{3}$
( ii)潜水员和Q点连线与竖直方向的夹角刚好为临界角C,则:sinC=$\frac{1}{n}$=$\frac{3}{4}$④
则得 cotC=$\frac{cosC}{sinC}$=$\sqrt{\frac{1-si{n}^{2}C}{sinC}}$=$\frac{\sqrt{7}}{3}$
又由几何知识解得:cotC=$\frac{{h}_{2}+△h}{{s}_{1}+{s}_{2}+l}$ ⑤
由④⑤得:l=($\frac{24}{7}\sqrt{7}$-3.8)m
答:(1)水的折射率n是$\frac{4}{3}$;
(2)赛艇的长度1为($\frac{24}{7}\sqrt{7}$-3.8)m.
点评 本题以光的直线传播为基础,利用几何知识,研究光传播到两种介质的界面时发生的反射、折射、全反射、色散等现象和它们表现的规律,即光的反射和折射定律,难点是光的全反射及其应用.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
17.如图所示是某电场区域的电场线分布,A、B、C、D 是电场中的四点,场强 E 的大小关系正确的是( )

| A. | EA<EC | B. | EB>ED | C. | EC<ED | D. | ED<EA |
18. 为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
 为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )| A. | 前内侧面的电势一定低于后内侧面的电势,与哪种离子多无关 | |
| B. | 若污水中正离子较多,则前内侧面比后内侧面的电势高 | |
| C. | 污水中离子浓度越高,电压表的示数越大 | |
| D. | 污水流量Q与电压U成正比,与ab无关 |
15.真空中两金属小球所带电荷量分别为+5Q和-Q,将它们接触后再分开,距离为r.真空中的静电力常量用k表示,则此时这两个金属小球之间的库仑力为( )
| A. | k$\frac{{Q}^{2}}{{r}^{2}}$ | B. | k$\frac{5{Q}^{2}}{{r}^{2}}$ | C. | k$\frac{4{Q}^{2}}{{r}^{2}}$ | D. | k$\frac{2{Q}^{2}}{{r}^{2}}$ |
12. 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )
 如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电的小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态.现给小球一竖直向上的初速度,小球最高能运动到M点.在小球从开始运动到运动至最高点时,以下说法正确的是( )| A. | 小球电势能的减少量等于小球重力势能的增加量 | |
| B. | 小球机械能的改变量等于电场力做的功 | |
| C. | 小球动能、电势能减少量之和等于弹性势能与小球重力势能增加量之和 | |
| D. | 弹性势能的增加量等于小球动能的减少量 |
19. 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.| A. | 每颗星做圆周运动的角速度为$\sqrt{\frac{3Gm}{{L}^{3}}}$ | |
| B. | 每颗星做圆周运动的加速度与三星的质量有关 | |
| C. | 若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍 | |
| D. | 若距离L和每颗星的质量m都变为原来的2倍,则线速度变为原来的4倍 |
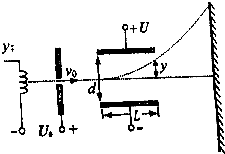 示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求:
示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求: