题目内容
1. 如图所示,物体A放在物体B上,B与轻弹簧相连,使它们一起在光滑水平面上的M、N两点之间做简谐运动.若从弹簧压缩到最短时开始计时(t=0),取向右为正方向,A所受静摩擦力f随时间t变化的图象正确的是( )
如图所示,物体A放在物体B上,B与轻弹簧相连,使它们一起在光滑水平面上的M、N两点之间做简谐运动.若从弹簧压缩到最短时开始计时(t=0),取向右为正方向,A所受静摩擦力f随时间t变化的图象正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 以AB整体为研究对象,得出加速度与振子位移的关系,再以A为研究对象,由牛顿第二定律分析f与加速度的关系,得到f与x的关系,选择图象.
解答 解:以AB整体为研究对象,根据牛顿第二定律得,加速度与振子位移的关系为a=-$\frac{kx}{{m}_{A}+{m}_{B}}$,再以A为研究对象,得到f=mAa=-$\frac{k{m}_{A}}{{m}_{A}+{m}_{B}}x$.
振子做简谐运动时,x随时间做正弦规律变化,当弹簧伸长到最短时开始记时时,t=0振子的位移为负向最大,则f为正向最大,所以图象为余弦函数.故B正确,ACD错误.
故选:B
点评 本题也可以直接简谐运动的特征F=-kx进行分析,关键分析t=0时刻的位移和回复力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11. 如图所示,底边长度相同的斜面AC和BC固定在水平地面CD上,一个小物块M与斜面AC、BC间动摩擦因数分别为μ1和μ2,物体M分别沿AC、BC从斜面顶端由静止下滑,最终都停在离C点距离相同的D点,假设两斜面在C点通过小圆弧与地面平滑相连,下列说法正确的是( )
如图所示,底边长度相同的斜面AC和BC固定在水平地面CD上,一个小物块M与斜面AC、BC间动摩擦因数分别为μ1和μ2,物体M分别沿AC、BC从斜面顶端由静止下滑,最终都停在离C点距离相同的D点,假设两斜面在C点通过小圆弧与地面平滑相连,下列说法正确的是( )
 如图所示,底边长度相同的斜面AC和BC固定在水平地面CD上,一个小物块M与斜面AC、BC间动摩擦因数分别为μ1和μ2,物体M分别沿AC、BC从斜面顶端由静止下滑,最终都停在离C点距离相同的D点,假设两斜面在C点通过小圆弧与地面平滑相连,下列说法正确的是( )
如图所示,底边长度相同的斜面AC和BC固定在水平地面CD上,一个小物块M与斜面AC、BC间动摩擦因数分别为μ1和μ2,物体M分别沿AC、BC从斜面顶端由静止下滑,最终都停在离C点距离相同的D点,假设两斜面在C点通过小圆弧与地面平滑相连,下列说法正确的是( )| A. | 物体沿斜面AC滑动到底端时动能较大 | |
| B. | 物体分别沿斜面AC和BC滑动到底端C时动能一样大 | |
| C. | μ1>μ2 | |
| D. | 物体沿两个斜面滑动过程中克服摩擦力做的功一样多 |
16.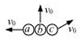 如图所示,完全相同的三个金属小球a、b、c位于距离地面同一高度处,现以等大的初速度使三个小球同时开始运动,分别做平抛、竖直上抛和斜抛运动,忽略空气阻力.以下说法不正确的是( )
如图所示,完全相同的三个金属小球a、b、c位于距离地面同一高度处,现以等大的初速度使三个小球同时开始运动,分别做平抛、竖直上抛和斜抛运动,忽略空气阻力.以下说法不正确的是( )
 如图所示,完全相同的三个金属小球a、b、c位于距离地面同一高度处,现以等大的初速度使三个小球同时开始运动,分别做平抛、竖直上抛和斜抛运动,忽略空气阻力.以下说法不正确的是( )
如图所示,完全相同的三个金属小球a、b、c位于距离地面同一高度处,现以等大的初速度使三个小球同时开始运动,分别做平抛、竖直上抛和斜抛运动,忽略空气阻力.以下说法不正确的是( )| A. | 落地之前,三个小球均做匀变速运动 | |
| B. | 落地之前,三个小球在任意相等时间内动量的增量相同 | |
| C. | b、c所能达到的最大高度相同 | |
| D. | 三个小球落地时的速度大小相等 |
6.关于原子核知识,下列描述正确的是( )
| A. | 温度升高,放射性元素衰变的半衰期减小 | |
| B. | 放射性物质$\left.\begin{array}{l}{238}\\{92}\end{array}\right.$U发生β衰变所释放的电子来源与核外电子 | |
| C. | 平均结合能越大,原子核越稳定 | |
| D. | 用中子轰击铀核,产生几个中等质量原子核的现象属于核聚变 |
13. 如图,甲、乙两水平圆盘紧靠在一块,甲圆盘为主动轮,乙靠摩擦随甲转动且无打滑.甲、乙圆盘的半径之比为r甲:r乙=3:1,两圆盘和小物体m1、m2之间的动摩擦因数相同,m1距圆心O点为2r,m2距圆心O′点为r,则( )
如图,甲、乙两水平圆盘紧靠在一块,甲圆盘为主动轮,乙靠摩擦随甲转动且无打滑.甲、乙圆盘的半径之比为r甲:r乙=3:1,两圆盘和小物体m1、m2之间的动摩擦因数相同,m1距圆心O点为2r,m2距圆心O′点为r,则( )
 如图,甲、乙两水平圆盘紧靠在一块,甲圆盘为主动轮,乙靠摩擦随甲转动且无打滑.甲、乙圆盘的半径之比为r甲:r乙=3:1,两圆盘和小物体m1、m2之间的动摩擦因数相同,m1距圆心O点为2r,m2距圆心O′点为r,则( )
如图,甲、乙两水平圆盘紧靠在一块,甲圆盘为主动轮,乙靠摩擦随甲转动且无打滑.甲、乙圆盘的半径之比为r甲:r乙=3:1,两圆盘和小物体m1、m2之间的动摩擦因数相同,m1距圆心O点为2r,m2距圆心O′点为r,则( )| A. | 当圆盘转速缓慢增加时,m2比m1先开始滑动 | |
| B. | 物块相对圆盘滑动前,m1与m2的角速度之比ω1:ω2=1:3 | |
| C. | 物块相对圆盘滑动前,m1与m2的线速度之比v1:v2=1:1 | |
| D. | 物块相对圆盘滑动前,m1与m2的向心加速度之比a1:a2=9:2 |
10.物体在做简谐运动的过程中,保持不变的物理量是( )
| A. | 速度 | B. | 动量 | C. | 机械能 | D. | 加速度 |
8.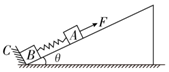 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,则( )| A. | 此过程中拉力F做功的大小等于物块A动能的增加量 | |
| B. | 当物块B刚要离开挡板时,受力满足m2gsinθ=kd | |
| C. | 当物块B刚要离开挡板时,物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 此过程中弹簧弹性势能的增加量为Fd-$\frac{1}{2}$m1v2-m1gdsinθ |
 如图所示,把一个带正电荷Q的小球A固定在绝缘支座上,另一个质量为m,带电量也为Q的带正电的小球B,用绝缘细线悬于O点,B球处于静止状态,细线与竖直方向的夹角为θ=30°,A、B均视为点电荷,已知A和B位于距地面高为h的水平线上且$\overrightarrow{AB}$=$\overrightarrow{OB}$.求:
如图所示,把一个带正电荷Q的小球A固定在绝缘支座上,另一个质量为m,带电量也为Q的带正电的小球B,用绝缘细线悬于O点,B球处于静止状态,细线与竖直方向的夹角为θ=30°,A、B均视为点电荷,已知A和B位于距地面高为h的水平线上且$\overrightarrow{AB}$=$\overrightarrow{OB}$.求: 如图所示,光滑水平面AB与竖直面内的半圆形光滑导轨在B点相切,半圆形导轨的半径R为5m.一个质量为10kg的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨之后沿导轨向上运动,恰能到达最高点C.(不计空气阻力,AB间足够长)试求:
如图所示,光滑水平面AB与竖直面内的半圆形光滑导轨在B点相切,半圆形导轨的半径R为5m.一个质量为10kg的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右的速度后脱离弹簧,当它经过B点进入导轨之后沿导轨向上运动,恰能到达最高点C.(不计空气阻力,AB间足够长)试求: