题目内容
12. 如图所示,把一个带正电荷Q的小球A固定在绝缘支座上,另一个质量为m,带电量也为Q的带正电的小球B,用绝缘细线悬于O点,B球处于静止状态,细线与竖直方向的夹角为θ=30°,A、B均视为点电荷,已知A和B位于距地面高为h的水平线上且$\overrightarrow{AB}$=$\overrightarrow{OB}$.求:
如图所示,把一个带正电荷Q的小球A固定在绝缘支座上,另一个质量为m,带电量也为Q的带正电的小球B,用绝缘细线悬于O点,B球处于静止状态,细线与竖直方向的夹角为θ=30°,A、B均视为点电荷,已知A和B位于距地面高为h的水平线上且$\overrightarrow{AB}$=$\overrightarrow{OB}$.求:(1)小球B所受到的库仑斥力及A、B两小球间的距离;
(2)A、B两小球在O点产生的合场强的大小及方向;
(3)剪断细线OB,小球B第一次落地时速度大小为v,求小球B的初位置和第一次落地点之间的电势差.
分析 (1)B球受到重力、线的拉力和电场力而平衡,根据B球受力平衡,由平衡条件求出库仑力,然后由库仑定律即可求出距离;
(2)根据库仑定律分析即可求出在O点产生的合场强的大小及方向;
(3)剪断细线OB,电场力与重力对b做功,由动能定理即可求出.
解答  解:(1)对B进行受力分析如图:
解:(1)对B进行受力分析如图:
则:F=mgtanθ=$\frac{\sqrt{3}}{3}mg$
由库仑定律:F=$\frac{k{Q}^{2}}{{r}^{2}}$
所以:r=$Q\sqrt{\frac{\sqrt{3}k}{mg}}$
(2)带电小球在O点产生的场强相等,都是:${E}_{A}={E}_{B}=\frac{kQ}{{r}^{2}}=\frac{\sqrt{3}mg}{3Q}$
合场强的方向在二者的角平分线上,大小为:${E}_{O}=2Ecos30°=\frac{mg}{Q}$,方向沿AB的中垂线向上
(3)小球B运动的过程中重力与电场力做功,由 动能定理得:
$mgh+QU=\frac{1}{2}m{v}^{2}$
所以:U=$\frac{m{v}^{2}-2mgh}{2Q}$
答:(1)小球B所受到的库仑斥力是$\frac{\sqrt{3}}{3}mg$,A、B两小球间的距离是$Q\sqrt{\frac{\sqrt{3}k}{mg}}$;
(2)A、B两小球在O点产生的合场强的大小是$\frac{mg}{Q}$,方向沿AB的中垂线向上;
(3)小球B的初位置和第一次落地点之间的电势差是$\frac{m{v}^{2}-2mgh}{2Q}$.
点评 对于复合场中的共点力作用下物体的平衡问题,其解决方法和纯力学中共点力作用下物体的平衡适用完全相同的解决方法,关键要正确分析受力情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
 如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )| A. | 粒子经偏转一定能回到原点O | |
| B. | 粒子在x轴上方和下方两磁场中运动的半径之比为1:2 | |
| C. | 粒子完成一次周期性运动的时间为$\frac{πm}{3qB}$ | |
| D. | 粒子第二次射入x轴上方磁场时,沿x轴前进3R |
20.在下面列举的各个实例中,哪些情况机械能是守恒的?( )
| A. | 汽车在水平面上匀速运动 | |
| B. | 羽毛球比赛中在空中运动的羽毛球 | |
| C. | 拉着物体沿光滑斜面匀速上升 | |
| D. | 如图所示,在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来 |
17. 如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )
如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )
 如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )
如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )| A. | v1:v2:v3=5:3:1 | |
| B. | 在C点落地的小球落地时的动能一定最大 | |
| C. | 三个小球落地的速度相同 | |
| D. | 三个小球下落的时间相同 |
4.以下说法中正确的是( )
| A. | 增透膜是利用了光的色散现象 | |
| B. | 电子表的液晶显示是利用了光的偏振现象 | |
| C. | 照相机镜头在阳光下呈现淡紫色是光的全发射现象 | |
| D. | 电视机遥控器是利用发出红外线脉冲信号来变换频道的 | |
| E. | 声波击碎玻璃杯的实验原理是共振 |
2.有些荧光物质在紫外线照射下会发出可见光,大额钞票的荧光防伪标志就是一例,下列说法正确的是( )
| A. | 改用红外线照射荧光物质也可以发出可见光 | |
| B. | 荧光物质发出的可见光的频率比红外线的频率低 | |
| C. | 荧光物质中的电子吸收了紫外线光子的能量 | |
| D. | 荧光物质发出可见光的过程是电子从低能级跃迁到高能级时产生的 |
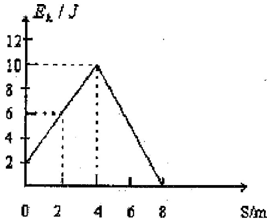 质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止.运动过程中物体动能随位移变化的Ek-s的图象如图所示.g取10m/s2.求:
质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止.运动过程中物体动能随位移变化的Ek-s的图象如图所示.g取10m/s2.求: 两轮平衡车(如图所示)广受年轻人的喜爱.它的动力系统由电池驱动,能够输出的最大功率为P0.小明驾驶平衡车在水平路面上沿直线运动时,受到的阻力恒为f,已知小明和平衡车的总质量为m,在以下讨论中,忽略小明身体姿态调整引起的重心位置的变化,并忽略小明对系统做的功.
两轮平衡车(如图所示)广受年轻人的喜爱.它的动力系统由电池驱动,能够输出的最大功率为P0.小明驾驶平衡车在水平路面上沿直线运动时,受到的阻力恒为f,已知小明和平衡车的总质量为m,在以下讨论中,忽略小明身体姿态调整引起的重心位置的变化,并忽略小明对系统做的功. 如图所示,物体A放在物体B上,B与轻弹簧相连,使它们一起在光滑水平面上的M、N两点之间做简谐运动.若从弹簧压缩到最短时开始计时(t=0),取向右为正方向,A所受静摩擦力f随时间t变化的图象正确的是( )
如图所示,物体A放在物体B上,B与轻弹簧相连,使它们一起在光滑水平面上的M、N两点之间做简谐运动.若从弹簧压缩到最短时开始计时(t=0),取向右为正方向,A所受静摩擦力f随时间t变化的图象正确的是( )


