题目内容
10.一个静止的质量为m1的不稳定的原子核,当它放射出质量为m2,速度为v的粒子后,剩余部分的速度应为( )| A. | -v | B. | -$\frac{{m}_{2}v}{{{m}_{1}-m}_{2}}$ | C. | -$\frac{{m}_{2}v}{{m}_{1}}$ | D. | -$\frac{{m}_{2}v}{{{m}_{1}+m}_{2}}$ |
分析 原子核衰变的过程可以认为系统动量守恒.根据动量守恒定律列出等式进行求解.
解答 解:根据动量守恒定律研究整个原子核:
0=m2v+(m1-m2)v′
解得:v′=$-\frac{{m}_{2}v}{{m}_{1}-{m}_{2}}$
故B正确,ACD错误.
故选:B.
点评 一般情况下我们运用动量守恒解决问题时要规定正方向,本题中速度中负号表示原子核剩余部分的速度方向与质量为m粒子速度方向相反.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
18. 对于如图所示的电流i随时间t作周期性变化的图象,下列说法中正确的是( )
对于如图所示的电流i随时间t作周期性变化的图象,下列说法中正确的是( )
 对于如图所示的电流i随时间t作周期性变化的图象,下列说法中正确的是( )
对于如图所示的电流i随时间t作周期性变化的图象,下列说法中正确的是( )| A. | 电流大小、方向都变化,是交流电 | B. | 电流大小变化,方向不变,是直流电 | ||
| C. | 电流大小变化,方向不变,是交流电 | D. | 电流最大值为0.2A,周期为0.02s |
5. 如图所示是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测.下列说法正确的是( )
如图所示是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测.下列说法正确的是( )
 如图所示是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测.下列说法正确的是( )
如图所示是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测.下列说法正确的是( )| A. | 发射“嫦娥一号”的速度必须达到第三宇宙速度 | |
| B. | 在绕月圆轨道上,卫星周期与卫星质量无关 | |
| C. | 卫星受月球的引力与它到月球中心距离的平方成反比 | |
| D. | 在绕月圆轨道上,卫星受月球的引力大于受到地球的引力 |
15. 如图,两光滑斜面在B处链接,小球由A处静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后的速度大小不变,则
如图,两光滑斜面在B处链接,小球由A处静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后的速度大小不变,则
( )
 如图,两光滑斜面在B处链接,小球由A处静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后的速度大小不变,则
如图,两光滑斜面在B处链接,小球由A处静止释放,经过B、C两点时速度大小分别为3m/s和4m/s,AB=BC.设球经过B点前后的速度大小不变,则( )
| A. | 球在AB、BC段的运动时间之比为7:4 | |
| B. | 球在AB、BC段的加速度大小之比为9:7 | |
| C. | 球在AB、BC段的重力做功之比为9:16 | |
| D. | 球由A运动到C的过程中平均速率为2.1m/s |
19.在水平面上有一物体在恒定的水平拉力F作用下移动了一段位移S,第一次在光滑的水平面上,第二次在粗糙的水平面上,则两次运动中拉力F所做的功( )
| A. | 一样多 | B. | 第一次多 | ||
| C. | 第二次多 | D. | 条件不足无法判断 |
20.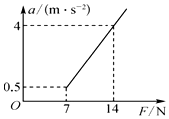 物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图所示.设最大静摩擦力与滑动摩擦力相等.根据题目提供的信息,下列说法中正确的是( )
物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图所示.设最大静摩擦力与滑动摩擦力相等.根据题目提供的信息,下列说法中正确的是( )
 物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图所示.设最大静摩擦力与滑动摩擦力相等.根据题目提供的信息,下列说法中正确的是( )
物体原来静止在水平地面上,用一水平力F拉物体,在F从0开始逐渐增大的过程中,物体先静止后又做变加速运动,其加速度a随外力F变化的图象如图所示.设最大静摩擦力与滑动摩擦力相等.根据题目提供的信息,下列说法中正确的是( )| A. | 物体的质量m=2kg | |
| B. | 物体与水平面间的动摩擦因数μ=0.6 | |
| C. | 物体与水平面的最大静摩擦力fmax=12N | |
| D. | 在F为10N时,物体的加速度a=2.0m/s2 |
 如图示的电阻不计且光滑的两平行金属导轨MN和OP放置在水平面内,MO间接有一阻值为R的电阻,导轨相距为d,其间有竖直向下的匀强磁场,磁感应强度大小为B,质量为m,电阻为r的导体棒CD垂直于导轨放置,并接触良好,现给导体棒CD一个水平初速度v,求:
如图示的电阻不计且光滑的两平行金属导轨MN和OP放置在水平面内,MO间接有一阻值为R的电阻,导轨相距为d,其间有竖直向下的匀强磁场,磁感应强度大小为B,质量为m,电阻为r的导体棒CD垂直于导轨放置,并接触良好,现给导体棒CD一个水平初速度v,求: 如图所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上(导轨电阻不计),导轨间距L=0.4m,导轨所在空间被分成区域Ⅰ和Ⅱ,两区域的边界与斜面的交线为MN.Ⅰ中的匀强磁场方向垂直斜面向下,Ⅱ中的匀强磁场方向垂直斜面向上,两磁场的磁感应强度大小均为B=0.5T.在区域Ⅰ中,将质量m1=0.1kg、电阻R1=0.1Ω的金属条ab放在导轨上.在区域Ⅱ中将质量m2=0.4kg,电阻R2=0.4Ω的光滑导体棒cd置于导轨上.当cd由静止开始下滑时,ab刚好不下滑,cd在滑动过程中始终处于区域Ⅱ的磁场中,ab、cd始终与导轨垂直且两端与导轨保持良好接触,取g=10m/s2,则在金属条ab出现滑动之前,求:
如图所示,两根足够长的平行金属导轨固定在倾角θ=30°的斜面上(导轨电阻不计),导轨间距L=0.4m,导轨所在空间被分成区域Ⅰ和Ⅱ,两区域的边界与斜面的交线为MN.Ⅰ中的匀强磁场方向垂直斜面向下,Ⅱ中的匀强磁场方向垂直斜面向上,两磁场的磁感应强度大小均为B=0.5T.在区域Ⅰ中,将质量m1=0.1kg、电阻R1=0.1Ω的金属条ab放在导轨上.在区域Ⅱ中将质量m2=0.4kg,电阻R2=0.4Ω的光滑导体棒cd置于导轨上.当cd由静止开始下滑时,ab刚好不下滑,cd在滑动过程中始终处于区域Ⅱ的磁场中,ab、cd始终与导轨垂直且两端与导轨保持良好接触,取g=10m/s2,则在金属条ab出现滑动之前,求: