题目内容
6.一宇航员登上月球,测得质量为m的物块的重为F0,已知月球的第一宇宙速度为v,不考虑月球的自转并视为匀质球,求月球的质量(引力常量为G).分析 在月球表面,不考虑月球的自转,物体的重力等于万有引力,据此列式;
月球的第一宇宙速度是月球表面卫星的环绕速度,根据万有引力等于向心力列式;
最后联立求解月球质量即可.
解答 解:设月球表面的重力加速度为g′,由重力与质量的关系得:
mg′=F0
设月球的质量为M、半径为R,由万有引力等于重力得:
$G\frac{Mm}{{R}^{2}}=mg′$
由万有引力等于向心力得:
$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$
联立解得:
M=$\frac{m{v}^{4}}{{F}_{0}G}$
答:月球的质量为$\frac{m{v}^{4}}{{F}_{0}G}$.
点评 对于卫星类问题,通常要抓住两点:在星球表面,重力等于万有引力;对卫星,万有引力提供向心力.

练习册系列答案
相关题目
3.某同学要测定一节旧电池的电动势和内电阻.实验器材仅有一个电流表、一个电阻箱、一个开关和导线若干,该同学按如图1所示电路进行实验,测得的数据如下表所示:
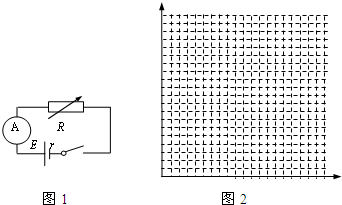
(1)若利用图象确定电池的电动势和内电阻,则应作R-$\frac{1}{I}$(选填“R-I”或“R-$\frac{1}{I}$”)图象;
(2)利用测得的数据在图2中的坐标纸上画出适当的图象;
(3)由图象可知,该电池的电动势E=6V,内阻r=2.0Ω.

| 次数 | 1 | 2 | 3 | 4 | 5 |
| R(Ω) | 4.0 | 10.0 | 16.0 | 22.0 | 28.0 |
| I(A) | 1.00 | 0.50 | 0.34 | 0.25 | 0.20 |
| $\frac{1}{I}$(A-1) | 1.0 | 2.0 | 2.9 | 4.0 | 5.0 |
(2)利用测得的数据在图2中的坐标纸上画出适当的图象;
(3)由图象可知,该电池的电动势E=6V,内阻r=2.0Ω.
17.月球绕地球做半径为R、周期为T的圆周运动,引力常量为G,根据已知条件可计算( )
| A. | 地球的质量 | B. | 月球的质量 | ||
| C. | 月球运动的向心加速度 | D. | 月球表面的重力加速度 |
14.一宇航员登陆到某星球上,若知道星球的质量为地球的2倍,直径也为地球的2倍,宇航员在地球上受到的万有引力大小为F,则他在该星球上受到的万有引力大小为( )
| A. | F | B. | 2F | C. | $\frac{F}{2}$ | D. | $\frac{F}{4}$ |
1.“嫦娥三号”探月卫星于2013年12月2日凌晨在西昌卫星发射中心发射,将实现“落月”的新阶段.若已知引力常量为G,月球绕地球做圆周运动的半径为r1、周期为T1,“嫦娥三号”探月卫星做圆周运动的环月轨道半径为r2、周期为T2,不计其他天体的影响,根据题目条件可以( )
| A. | 求出月球的质量 | B. | 求出“嫦娥三号”探月卫星的质量 | ||
| C. | 得出$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | D. | 求出地球的密度 |
18.假设月球绕地球的运动为匀速圆周运动.已知万有引力常量为G,下列物理量中可以求出地球质量的是( )
| A. | 月球表面重力加速度和月球到地球的距离 | |
| B. | 地球表面的重力加速度和月球到地球的距离 | |
| C. | 月球绕地球运动的线速度和周期 | |
| D. | 月球的质量和月球到地球的距离 |
15.关于曲线运动,下列说法中正确的是( )
| A. | 在平衡力作用下,物体可以做曲线运动 | |
| B. | 曲线运动的加速度可以一直为零 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 在恒力作用下,物体不可以做曲线运动 |
16.一只“220V,100W”的灯泡接在u=311sin 314t V的交变电源上,则下列判断正确的是( )
| A. | 灯泡不能正常发光 | |
| B. | 与灯泡串联的电流表的示数为0.45 A | |
| C. | 与灯泡并联的电压表的示数为220 V | |
| D. | 通过灯泡的电流的表达式为i=0.64 sin 314t A |