题目内容
14. 如图所示,弯折的直角轻杆ABCO通过铰链O连接在地面上,AB=BC=OC=9m,一质量为m的小滑块以足够大的初始速度,在杆上从C点左侧x0=2m处向左运动,作用于A点的水平向右拉力F可以保证BC始终水平.若滑块与杆之间的动摩擦因数与离开C点的距离x满足μx=1,则滑块的运动位移s=3m时拉力F达到最小.若滑块的初始速度v0=5m/s,且μ=0.5-0.1x(μ=0后不再变化),则滑块达到C点左侧x=4m处时,速度减为v=1m/s.
如图所示,弯折的直角轻杆ABCO通过铰链O连接在地面上,AB=BC=OC=9m,一质量为m的小滑块以足够大的初始速度,在杆上从C点左侧x0=2m处向左运动,作用于A点的水平向右拉力F可以保证BC始终水平.若滑块与杆之间的动摩擦因数与离开C点的距离x满足μx=1,则滑块的运动位移s=3m时拉力F达到最小.若滑块的初始速度v0=5m/s,且μ=0.5-0.1x(μ=0后不再变化),则滑块达到C点左侧x=4m处时,速度减为v=1m/s.
分析 滑块向左做减速运动,对杆有压力和向左的滑动摩擦力,对杆,以点O为支点,根据力矩平衡条件列式求解拉力的F的表达式进行分析;
若滑块的初始速度v0=5m/s,对滑块向左运动过程根据动能定理列式求解达到C点左侧x=4m处时速度.
解答 解:滑块向左做减速运动,对杆有压力和向左的滑动摩擦力;
对杆,根据力矩平衡条件,有:F•2BC=mg•x+μmg•CO;
代入数据和μx=1,有:F=$\frac{1}{2}mg(\frac{x}{9}+\frac{1}{x})$
当$\frac{x}{9}=\frac{1}{x}$,即x=3m(=s)时,拉力F达到最小;
滑块从C点达到C点左侧x=4m处过程,根据动能定理,有:
-$\overline{f}$•x=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$
其中:$\overline{f}$=$\frac{{μ}_{0}+{μ}_{1}}{2}•mg$
联立解得:$v=\sqrt{{v}_{0}^{2}-({μ}_{1}+{μ}_{2})gx}$=$\sqrt{{5}^{2}-[0.5+(0.5-0.1×4)]×10×4}$m/s=1m/s;
故答案为:3,1.
点评 本题是力学综合问题,第一空在受力分析时不要忘了滑动摩擦力,第二空动摩擦因数可以采用平均值进行计算,较难.

练习册系列答案
相关题目
19. 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右运动,刚好使A向上做匀速直线运动的过程中,则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右运动,刚好使A向上做匀速直线运动的过程中,则( )
 如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右运动,刚好使A向上做匀速直线运动的过程中,则( )
如图所示,物体A和B的质量均为m,且分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦),在用水平变力F拉物体B沿水平方向向右运动,刚好使A向上做匀速直线运动的过程中,则( )| A. | 物体B在水平方向向右也做匀速直线运动 | |
| B. | 物体B在水平方向向右的做减速运动 | |
| C. | 绳子拉力大于物体A所受重力 | |
| D. | 绳子拉力小于物体A所受重力 |
20.“嫦娥一号”和“嫦娥二号”两颗月球探测卫星,它们绕月的圆形轨道距月球表面分别约为200km和100km.当它们在绕月轨道上运行时,两者相比,“嫦娥二号”的( )
| A. | 周期较小 | B. | 周期相同 | C. | 向心加速度相同 | D. | 向心加速度较小 |
3.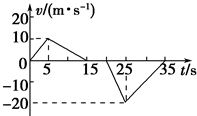 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )| A. | 在0~15s内,观光电梯上升的高度为25m | |
| B. | 在0~35s内,观光电梯的平均速率为6m/s | |
| C. | 在20~25s与25~35 s内,观光电梯的平均速度大小均为10m/s | |
| D. | 在25~35s内,观光电梯在减速上升,该同学的加速度大小为2m/s2 |
 如图所示,倾斜传送带与水平面夹角为30°,并以v0=3m/s顺时针匀速运行,在传送带的底部A端轻轻放一个m=0.4kg可视为质点的小滑块,已知小滑块与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,传送带AB长L=7.2m.若取沿传送带向上为正方向,取g=10m/s2,则下列描述小滑块在传送带上运动时的摩擦力f,位移x,速度v和摩擦力的功率P随时间t的变化图象中正确的有( )
如图所示,倾斜传送带与水平面夹角为30°,并以v0=3m/s顺时针匀速运行,在传送带的底部A端轻轻放一个m=0.4kg可视为质点的小滑块,已知小滑块与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,传送带AB长L=7.2m.若取沿传送带向上为正方向,取g=10m/s2,则下列描述小滑块在传送带上运动时的摩擦力f,位移x,速度v和摩擦力的功率P随时间t的变化图象中正确的有( )



 研究平抛物体的运动”实验的装置如图所示,在实验前应A.
研究平抛物体的运动”实验的装置如图所示,在实验前应A.
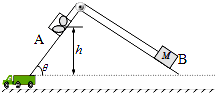 如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.
如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.