题目内容
1.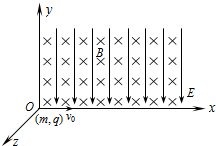 如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求:
如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求:(1)此带电粒子距x轴的最大距离;
(2)此带电粒子的轨迹与x轴相切的所有点的坐标x所满足的条件.
分析 (1)粒子的运动可以看做匀速直线运动与匀速圆周运动,根据粒子在磁场中做圆周运动的轨道半径与周期公式求出最大距离.
(2)作出粒子运动轨迹,应用运动学公式求出粒子沿x轴的位移,然后分析答题.
解答 解:(1)令v0=v1+v′=$\frac{2E}{B}$,其中v1=$\frac{E}{B}$,v′=$\frac{E}{B}$其方向与v0方向相同.
则带电粒子的运动可视为速度为v1=$\frac{E}{B}$的匀速直线运动与速度为v′的逆时针方向的匀速圆周运动的合运动,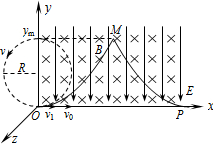
运动轨迹如图所示,其圆周运动的半径和周期分别为:R=$\frac{mv′}{qB}$=$\frac{mE}{q{B}^{2}}$,T=$\frac{2πm}{qB}$,
故带电粒子将做螺旋线运动,粒子运动的轨迹如图中实线所示,
M点为粒子距x轴的最远点.在这一点粒子的速度:vM=v1-v′=0,
它到x轴的距离为:ym=2R=$\frac{2mE}{q{B}^{2}}$;
(2)如图P点为粒子运动轨迹与x轴的相切点,
且粒子在该点的速度为:vP=v1+v′=$\frac{2E}{B}$,
其与x轴的切点坐标为:xp=v1T=$\frac{E}{B}$×$\frac{2πm}{qB}$=$\frac{2πmE}{q{B}^{2}}$,
根据运动的周期性,粒子与x轴的所有相切点的坐标为
x=nxp=v1nT=$\frac{E}{B}$×n$\frac{2πm}{qB}$=$\frac{2nπmE}{q{B}^{2}}$ (n=1、2、3、…);
答:(1)此带电粒子距x轴的最大距离为$\frac{2mE}{q{B}^{2}}$;
(2)此带电粒子的轨迹与x轴相切的所有点的坐标x所满足的条件是:$\frac{2nπmE}{q{B}^{2}}$ (n=1、2、3、…).
点评 本题考查了粒子在电场与磁场中的运动,应用运动的合成与分解观点是解题的关键,分析清楚粒子运动过程、作出粒子运动轨迹,应用圆周运动的轨道半径公式与周期公式、应用运动学公式可以解题.

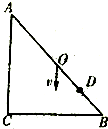 如图所示,等腰直角三角形,ABC内部存在垂直于纸面的匀强磁场,三个比荷相同的粒子从AB边的中点O点竖直向下射入磁场,分别从B点、C点和D点离开磁场,不计带电粒子受到的重力,D点为OB间的一点,下列说法错误的是( )
如图所示,等腰直角三角形,ABC内部存在垂直于纸面的匀强磁场,三个比荷相同的粒子从AB边的中点O点竖直向下射入磁场,分别从B点、C点和D点离开磁场,不计带电粒子受到的重力,D点为OB间的一点,下列说法错误的是( )| A. | 从B点到C点离开的带电粒子的速度大小相等,电性相反 | |
| B. | 三个带电粒子在磁场中运动的时间相同 | |
| C. | 从D点离开磁场的带电粒子在磁场运动的时间比从B点离开的粒子少 | |
| D. | 从D点离开磁场的带电粒子的速率比从B点离开的粒子小 |
| A. | 导体棒离开磁场时速度大小为$\frac{2mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| B. | 导体棒经过磁场的过程中,通过电阻R的电荷量为$\frac{5BLd}{R}$ | |
| C. | 离开磁场时导体棒两端电压为$\frac{2mgR}{BL}$ | |
| D. | 导体棒经过磁场的过程中,电阻R产生焦耳热为$\frac{9mgdR{B}^{4}{L}^{4}-2{m}^{3}{g}^{2}R(R+r)^{2}}{{B}^{4}{L}^{4}(R+r)}$ |
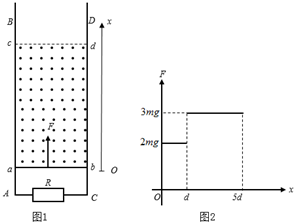
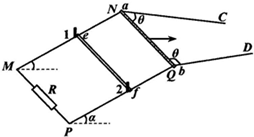 如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.
如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g. 如图所示,在第Ⅱ象限内有水平向右的匀强电场,在第Ⅰ象存在如图所示的匀强磁场.有一个带电量为q、质量为m的粒子以初速度v0垂直于x轴从P点进入匀强电场中,并从y轴的Q点(图中未画出)与正方向成45°角进入磁场,又恰好垂直于x轴射出磁场.已知OP之间的距离为d,(不计粒子重力),求
如图所示,在第Ⅱ象限内有水平向右的匀强电场,在第Ⅰ象存在如图所示的匀强磁场.有一个带电量为q、质量为m的粒子以初速度v0垂直于x轴从P点进入匀强电场中,并从y轴的Q点(图中未画出)与正方向成45°角进入磁场,又恰好垂直于x轴射出磁场.已知OP之间的距离为d,(不计粒子重力),求 如图,半径为r=10cm的匀强磁场区域边界跟y轴相切于坐标原点O,磁感强度B=0.332T,方向垂直纸面向里.在O处有一放射源S,可向纸面各个方向射出速度为v=3.2×106m/s的粒子.已知α粒子质量m=6.64×10-27kg,电量q=3.2×10-19C,试画出α粒子通过磁场空间做圆周运动的圆心轨道,求出α粒子通过磁场空间的最大偏角.
如图,半径为r=10cm的匀强磁场区域边界跟y轴相切于坐标原点O,磁感强度B=0.332T,方向垂直纸面向里.在O处有一放射源S,可向纸面各个方向射出速度为v=3.2×106m/s的粒子.已知α粒子质量m=6.64×10-27kg,电量q=3.2×10-19C,试画出α粒子通过磁场空间做圆周运动的圆心轨道,求出α粒子通过磁场空间的最大偏角. 如图所示,经电压U加速的电子(加速前电子静止),从电子枪口T射出,其初速沿直线Ta的方向.若要求电子能击中与枪口有一定距离的靶M点,且有如图所示的θ夹角.第一次用磁感强度为B的匀强磁场覆盖电子所经过的空间就可以达到此目的,磁场方向与纸面垂直;若第二次在该空间只加匀强电场,场强方向与纸面平行且与Ta垂直,电子同样能打中M点,设电子质量为m电量为e,求匀强电场的场强E=?(用题中所给条件量表示)
如图所示,经电压U加速的电子(加速前电子静止),从电子枪口T射出,其初速沿直线Ta的方向.若要求电子能击中与枪口有一定距离的靶M点,且有如图所示的θ夹角.第一次用磁感强度为B的匀强磁场覆盖电子所经过的空间就可以达到此目的,磁场方向与纸面垂直;若第二次在该空间只加匀强电场,场强方向与纸面平行且与Ta垂直,电子同样能打中M点,设电子质量为m电量为e,求匀强电场的场强E=?(用题中所给条件量表示)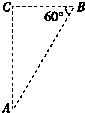 如图所示,A、B、C三点都在匀强电场中.已知AC⊥BC,∠ABC=60°,BC=20cm.把一个q=10-5 C的正电荷从A移到B,电场力做功为零;从B移到C,电场力做功为-1.73×10-3 J,则该匀强电场的场强大小是1000V/m,并在图中作出过C点电场线和等势面.
如图所示,A、B、C三点都在匀强电场中.已知AC⊥BC,∠ABC=60°,BC=20cm.把一个q=10-5 C的正电荷从A移到B,电场力做功为零;从B移到C,电场力做功为-1.73×10-3 J,则该匀强电场的场强大小是1000V/m,并在图中作出过C点电场线和等势面.