题目内容
13. 如图,半径为r=10cm的匀强磁场区域边界跟y轴相切于坐标原点O,磁感强度B=0.332T,方向垂直纸面向里.在O处有一放射源S,可向纸面各个方向射出速度为v=3.2×106m/s的粒子.已知α粒子质量m=6.64×10-27kg,电量q=3.2×10-19C,试画出α粒子通过磁场空间做圆周运动的圆心轨道,求出α粒子通过磁场空间的最大偏角.
如图,半径为r=10cm的匀强磁场区域边界跟y轴相切于坐标原点O,磁感强度B=0.332T,方向垂直纸面向里.在O处有一放射源S,可向纸面各个方向射出速度为v=3.2×106m/s的粒子.已知α粒子质量m=6.64×10-27kg,电量q=3.2×10-19C,试画出α粒子通过磁场空间做圆周运动的圆心轨道,求出α粒子通过磁场空间的最大偏角.
分析 从O点射入后,运动轨迹对应的弦最大,则α粒子通过磁场空间的偏角最大,因此弦最长即为直径,从而即可求解.
解答  解:根据运动轨迹半径公式有:R=$\frac{mv}{Bq}$,
解:根据运动轨迹半径公式有:R=$\frac{mv}{Bq}$,
代入数据,解得:R=0.2m;
粒子在磁场中作圆周运动,转过的圆心角有最大值时,对于的弦长为磁场区域圆的直径,由右图,图中三角形刚好是等边三角形,
则有:α=60°;
因此粒子在磁场中运动的速度的最大偏转角也是60°;
答:α粒子通过磁场空间的最大偏角为60°.
点评 该题考查到了带电粒子在匀强磁场中做圆周运动的半径的推导,洛伦兹力提供向心力;带电粒子在圆形区域的匀强磁场中的偏转角,与在磁场中的弧长是成正比的,弧长越长,所对应的弦长也就越长,要会熟练的利用几何关系求解圆心角;对于由于有限制条件使得粒子多次在磁场中运动的情况,要彻底分析粒子的运动过程,分析其运动规律.

练习册系列答案
相关题目
18.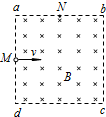 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
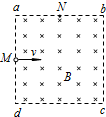 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )| A. | a点 | B. | b点 | C. | 在N、a之间某点 | D. | 在N、b之间某点 |
5. 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )| A. | a粒子的速度比b粒子速度小 | |
| B. | a粒子在磁场中的运动时间比b粒子短 | |
| C. | 两粒子离开磁场时的速度反向延长线一定都过圆心 | |
| D. | 两粒子离开磁场时的速度反向延长线不一定都过圆心 |
2.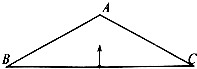 顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
 顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )| A. | 1:3 | B. | 1:2 | C. | (2$\sqrt{3}-3$):1 | D. | 1:1 |
3.关于电场线的下列说法中错误的是( )
| A. | 电场线并非真实存在,是假想出来的,既能反映电场的强弱,也能反映电场的方向 | |
| B. | 电场线处处与等势面垂直 | |
| C. | 只要初速度为零,正电荷必将沿电场线方向移动 | |
| D. | 负电荷所受电场力方向一定与电场线切线方向相反 |
 如图甲所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x 轴放置一块平行y轴且沿y轴负向足够长的竖直平板C3,平板C3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=4$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔,进入磁场区域.已知小球可视为质点,小球的比荷$\frac{q}{m}$=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=$\frac{{\sqrt{2}}}{10}$m,不考虑空气阻力.求:
如图甲所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x 轴放置一块平行y轴且沿y轴负向足够长的竖直平板C3,平板C3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=4$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔,进入磁场区域.已知小球可视为质点,小球的比荷$\frac{q}{m}$=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=$\frac{{\sqrt{2}}}{10}$m,不考虑空气阻力.求: 如图所示,在xOy平面内存在I、II、III、IV四个场区,y轴右侧存在匀强磁场I,y轴左侧与虚线MN之间存在方向相反的两个匀强电场,II区电场方向竖直向下,III区电场方向竖直向上,P点是MN与x轴的交点.有一质量为m,带电荷量+q的带电粒子由原点O,以速度v0沿x轴正方向水平射入磁场I,已知匀强磁场I的磁感应强度垂直纸面向里,大小为2B0,匀强电场II和匀强电场III的电场强度大小均为E=$\frac{{{B_0}{v_0}}}{2}$,如图所示,IV区的磁场垂直纸面向外,大小为B0,OP之间的距离为$\frac{{4m{v_0}}}{{q{B_0}}}$,已知粒子最后能回到O点.
如图所示,在xOy平面内存在I、II、III、IV四个场区,y轴右侧存在匀强磁场I,y轴左侧与虚线MN之间存在方向相反的两个匀强电场,II区电场方向竖直向下,III区电场方向竖直向上,P点是MN与x轴的交点.有一质量为m,带电荷量+q的带电粒子由原点O,以速度v0沿x轴正方向水平射入磁场I,已知匀强磁场I的磁感应强度垂直纸面向里,大小为2B0,匀强电场II和匀强电场III的电场强度大小均为E=$\frac{{{B_0}{v_0}}}{2}$,如图所示,IV区的磁场垂直纸面向外,大小为B0,OP之间的距离为$\frac{{4m{v_0}}}{{q{B_0}}}$,已知粒子最后能回到O点.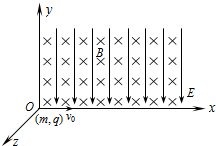 如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求:
如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求: 如图所示,小球的质量为m,带电量为q,悬挂小球的丝线与竖直方向成θ角时,小球恰好在匀强电场中静止不动,丝线长度为l.
如图所示,小球的质量为m,带电量为q,悬挂小球的丝线与竖直方向成θ角时,小球恰好在匀强电场中静止不动,丝线长度为l.