题目内容
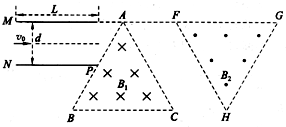
10. 如图所示,经电压U加速的电子(加速前电子静止),从电子枪口T射出,其初速沿直线Ta的方向.若要求电子能击中与枪口有一定距离的靶M点,且有如图所示的θ夹角.第一次用磁感强度为B的匀强磁场覆盖电子所经过的空间就可以达到此目的,磁场方向与纸面垂直;若第二次在该空间只加匀强电场,场强方向与纸面平行且与Ta垂直,电子同样能打中M点,设电子质量为m电量为e,求匀强电场的场强E=?(用题中所给条件量表示)
如图所示,经电压U加速的电子(加速前电子静止),从电子枪口T射出,其初速沿直线Ta的方向.若要求电子能击中与枪口有一定距离的靶M点,且有如图所示的θ夹角.第一次用磁感强度为B的匀强磁场覆盖电子所经过的空间就可以达到此目的,磁场方向与纸面垂直;若第二次在该空间只加匀强电场,场强方向与纸面平行且与Ta垂直,电子同样能打中M点,设电子质量为m电量为e,求匀强电场的场强E=?(用题中所给条件量表示)
分析 电场力对电子做功,电子的动能增大;根据动能定理可求得出射速度;电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,求得电子的运动半径;明确几何关系;再根据电子在电场中做类平抛运动,根据运动的合成和分解规律可明确要击中M点应施加的电场强度.
解答  解:电子在电场中被加速eU=$\frac{1}{2}$mv02,所以v0=$\sqrt{\frac{2eU}{m}}$
解:电子在电场中被加速eU=$\frac{1}{2}$mv02,所以v0=$\sqrt{\frac{2eU}{m}}$
粒子在磁场中运动轨迹如图所示;
由洛伦兹力提供向心力Bev0=m$\frac{{v}_{0}^{2}}{R}$得
在磁场中R=$\frac{m{v}_{0}}{Be}$=$\frac{1}{B}$$\sqrt{\frac{2mv}{e}}$
设TM之间距离为d,有R=$\frac{\frac{d}{2}}{sinθ}$=$\frac{d}{2sinθ}$
在电场中有x=dcosθ=v0t
y=dsinθ=$\frac{1}{2}$•$\frac{Ee}{m}$t2
消去t,d:电场强度E=$\frac{B}{co{s}^{2}θ}$$\sqrt{\frac{2eU}{m}}$
答:匀强电场的场强为$\frac{B}{co{s}^{2}θ}$$\sqrt{\frac{2eU}{m}}$
点评 本题考查电子在电场中加速,在磁场中偏转的问题分析,解题的关键是电子在磁场中做圆周运动,在电场中做类平抛运动,明确对应的几何关系和平抛运动的运动的合成和分解规律是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.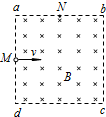 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
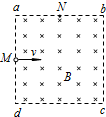 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )| A. | a点 | B. | b点 | C. | 在N、a之间某点 | D. | 在N、b之间某点 |
5. 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
 如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )
如图所示,速度不同的同种带电粒子(重力都不计)a、b沿半径AO方向进入一圆形匀强磁场区域,a、b两粒子的运动轨迹分别为AB和AC,则下列说法中正确的是( )| A. | a粒子的速度比b粒子速度小 | |
| B. | a粒子在磁场中的运动时间比b粒子短 | |
| C. | 两粒子离开磁场时的速度反向延长线一定都过圆心 | |
| D. | 两粒子离开磁场时的速度反向延长线不一定都过圆心 |
15. 如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
 如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )
如图所示,一平行板电容器的电容为C,两极板M、N间距离为d,所接电源的电动势为E,两板间a、b、c三点的连线构成一等腰直角三角形.三角形的两直角边长均为L,其中ab边与两板平行,以下说法正确的是( )| A. | 电容器所带电荷量为2CE | |
| B. | 两极板间匀强电场的电场强度大小为$\frac{E}{d}$ | |
| C. | a、c两点间的电势差为$\frac{\sqrt{2}EL}{d}$ | |
| D. | 若增大两板间距离时,a、c两点间电势差不变 |
2.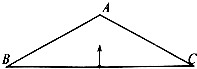 顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
 顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )
顶角A为120°的等腰三角形ABC内部有匀强磁场,磁场垂直三角形所在平面,如图所示,一对正负电子由底边BC中点沿垂直于底边的方向射入磁场中,正电子恰能从底边BC射出,负电子恰好垂直打到AC边,不计两电子间的相互作用力和重力,正负电子的速率之比为( )| A. | 1:3 | B. | 1:2 | C. | (2$\sqrt{3}-3$):1 | D. | 1:1 |
20.关于静摩擦力下列说法中正确的是( )
| A. | 静摩擦力的方向与物体的运动方向相反 | |
| B. | 静摩擦力大小与压力成正比 | |
| C. | 受静摩擦力作用的物体一定是静止的 | |
| D. | 静摩擦力不一定是阻力 |
 如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m、电荷量为q的带电粒子在坐标为($\frac{7}{4}L$,$\frac{{\sqrt{7}}}{2}L$)的A点,以初速度$\frac{v_0}{2}$沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,不计粒子重力.(结果里可以有根号)
如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m、电荷量为q的带电粒子在坐标为($\frac{7}{4}L$,$\frac{{\sqrt{7}}}{2}L$)的A点,以初速度$\frac{v_0}{2}$沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,不计粒子重力.(结果里可以有根号)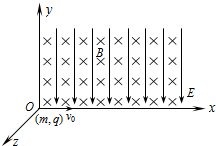 如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求:
如图所示,空间匀强电场E沿-y方向,匀强磁场B沿-z方向.有一电荷量为q,质量为m的带正电粒子,从O点沿+x轴方向以初速度v0=$\frac{2E}{B}$射入场区,粒子的重力忽略不计,求: