题目内容
14.质量m=0.60kg的篮球从距地板H=0.80m高处由静止释放,与水平地板撞击后反弹上升的最大高度h=0.45m,从释放到弹跳至h高处经历的时间t=1.1s,忽略空气阻力,重力加速度g=10m/s2,求:(1)篮球与地板撞击过程中损失的机械能;
(2)篮球对地板的平均撞击力.
分析 (1)篮球与地板撞击过程中损失的机械能等于初始时刻机械能减去末时刻机械能,初末位置物体动能为零,只有势能;
(2)分别根据自由落体运动求出篮球与地面碰撞前后的速度,再求出下落和上升的时间,根据总时间求出球与地面接触的时间,根据动量定律即可求解.
解答 解:(1)篮球与地板撞击过程中损失的机械能为:△E=mgH-mgh=0.6×10×(0.8-0.45)J=2.1J
(2)设篮球从H高处下落到地板所用时间为t1,刚接触地板时的速度为v1;反弹离地时的速度为v2,上升的时间为t2,由动能定理和运动学公式
下落过程:mgH=$\frac{1}{2}{{mv}_{1}}^{2}$,解得:v1=4m/s,${t}_{1}=\frac{{v}_{1}}{g}=0.4s$
上升过程:-mgh=0-$\frac{1}{2}{{mv}_{2}}^{2}$,解得:v2=3m/s,${t}_{2}=\frac{{v}_{2}}{g}=0.3s$
篮球与地板接触时间为△t=t-t1-t2=0.4s
设地板对篮球的平均撞击力为F,取向上为正方向,由动量定理得:
(F-mg)△t=mv2-(-mv1)
解得:F=16.5N
根据牛顿第三定律,篮球对地板的平均撞击力 F′=F=16.5N,方向向下
答:(1)篮球与地板撞击过程中损失的机械能为2.1J.
(2)篮球对地板的平均撞击力为16.5N,方向向下.
点评 本题主要考查了自由落体运动的基本规律,在与地面接触的过程中,合外力对物体的冲量等于物体动量的变化量,难度适中.

练习册系列答案
相关题目
4.下列核反应中属于重核裂变的是( )
| A. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| B. | ${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{54}^{140}$Xe+${\;}_{38}^{94}$Sr+2${\;}_{0}^{1}$n | |
| C. | ${\;}_{88}^{226}$Ra→${\;}_{86}^{222}$Rn+${\;}_{2}^{4}$He | |
| D. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+${\;}_{-1}^{0}$e |
2. 如图所示为A、B两部分理想气体的V-t图象,设两部分气体是质量相同的同种气体,根据图中所给条件,可知( )
如图所示为A、B两部分理想气体的V-t图象,设两部分气体是质量相同的同种气体,根据图中所给条件,可知( )
 如图所示为A、B两部分理想气体的V-t图象,设两部分气体是质量相同的同种气体,根据图中所给条件,可知( )
如图所示为A、B两部分理想气体的V-t图象,设两部分气体是质量相同的同种气体,根据图中所给条件,可知( )| A. | 当t=273.15℃时,A气体的体积比B气体的体积大0.2 m3 | |
| B. | 当tA=tB时,VA:VB=3:1 | |
| C. | 当tA=tB时,VA:VB=1:3 | |
| D. | A、B两部分气体都发生等压变化,它们的压强之比pA:pB=3:1 |
3.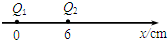 如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-10-8C,分别固定在x坐标轴的x=0和x=6cm的位置上,取无穷远点电势为零.则下列说法正确的是( )
如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-10-8C,分别固定在x坐标轴的x=0和x=6cm的位置上,取无穷远点电势为零.则下列说法正确的是( )
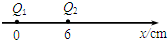 如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-10-8C,分别固定在x坐标轴的x=0和x=6cm的位置上,取无穷远点电势为零.则下列说法正确的是( )
如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-10-8C,分别固定在x坐标轴的x=0和x=6cm的位置上,取无穷远点电势为零.则下列说法正确的是( )| A. | 除无穷远外,x坐标轴上只有一个电场强度为零的点 | |
| B. | x坐标轴上电场强度方向沿x轴正方向区域是(0,6cm)和(12cm,∞) | |
| C. | 过x=3cm的x轴的中垂线是一条等势线 | |
| D. | 在x轴上x>6cm的区域,电势φ>0. |
4.下列关于机械能是否守恒的叙述中正确的是( )
| A. | 做匀速直线运动的物体机械能一定守恒 | |
| B. | 做匀变速运动的物体机械能可能守恒 | |
| C. | 外力对物体做功为零时,物体的机械能一定守恒 | |
| D. | 系统内只有重力和弹簧的弹力做功时,系统的机械能一定守恒 |

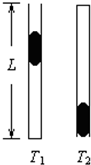 如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为T1.现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为1:3.若将管内下部气体温度降至T2,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出).已知T1=2.5T2,大气压强为P0,重力加速度为g.求水银柱的长度h和水银的密度ρ.
如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为T1.现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为1:3.若将管内下部气体温度降至T2,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出).已知T1=2.5T2,大气压强为P0,重力加速度为g.求水银柱的长度h和水银的密度ρ.