题目内容
9.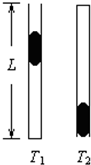 如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为T1.现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为1:3.若将管内下部气体温度降至T2,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出).已知T1=2.5T2,大气压强为P0,重力加速度为g.求水银柱的长度h和水银的密度ρ.
如图所示,一竖直放置的、长为L的细管下端封闭,上端与大气(视为理想气体)相通,初始时管内气体温度为T1.现用一段水银柱从管口开始注入管内将气柱封闭,该过程中气体温度保持不变且没有气体漏出,平衡后管内上下两部分气柱长度比为1:3.若将管内下部气体温度降至T2,在保持温度不变的条件下将管倒置,平衡后水银柱下端与管下端刚好平齐(没有水银漏出).已知T1=2.5T2,大气压强为P0,重力加速度为g.求水银柱的长度h和水银的密度ρ.
分析 注入水银的过程,下部分气体发生等温变化,根据玻意耳定律列出方程;将管倒置后,温度降低的过程,管内气体的三个参量都发生变化,根据气态方程列式,再联立求解.
解答 解:设管内截面面积为S,初始时气体压强为p0,体积为:V0=LS; 注入水银后下部气体压强为:p1=p0+ρgh;体积为:V1=$\frac{3}{4}$(L-h)S
由玻意耳定律有:p0LS=(p0+ρgh)×$\frac{3}{4}$(L-h)S…①
将管倒置后,管内气体压强为 p2=p0-ρgh;体积为:V2=(L-h)S
由理想气体状态方程有:$\frac{{p}_{0}LS}{{T}_{1}}$=$\frac{({p}_{0}-ρgh)(L-h)S}{{T}_{2}}$…②
由①、②解得:h=$\frac{2}{15}$L,ρ=$\frac{105{p}_{0}}{26gL}$
答:水银柱的长度h为$\frac{2}{15}$L,水银的密度ρ是$\frac{105{p}_{0}}{26gL}$.
点评 本题关键是求解出初状态和末状态气体的压强,然后根据玻意耳定律和气态方程列出方程,进行求解.

练习册系列答案
相关题目
17. 航天器完成维修地球高轨道卫星任务后,在A点从圆形轨道Ⅰ进入椭圆形轨道Ⅱ,B点为椭圆形轨道Ⅱ的近地点,如图所示.关于航天器的运动,下列说法中正确的有( )
航天器完成维修地球高轨道卫星任务后,在A点从圆形轨道Ⅰ进入椭圆形轨道Ⅱ,B点为椭圆形轨道Ⅱ的近地点,如图所示.关于航天器的运动,下列说法中正确的有( )
 航天器完成维修地球高轨道卫星任务后,在A点从圆形轨道Ⅰ进入椭圆形轨道Ⅱ,B点为椭圆形轨道Ⅱ的近地点,如图所示.关于航天器的运动,下列说法中正确的有( )
航天器完成维修地球高轨道卫星任务后,在A点从圆形轨道Ⅰ进入椭圆形轨道Ⅱ,B点为椭圆形轨道Ⅱ的近地点,如图所示.关于航天器的运动,下列说法中正确的有( )| A. | 在轨道Ⅱ上经过A点时的速度大于经过B点时的速度 | |
| B. | 从轨道Ⅰ进入轨道Ⅱ时航天器要在A点制动减速 | |
| C. | 在轨道Ⅰ上经过A点时的加速度等于轨道Ⅱ经过A点时的加速度 | |
| D. | 在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期 |
4. 如图所示,两容器用水平细管相连,容器内充有温度为T的同种气体被一小段水银隔成A、B两部分,现使A、B同时升高温度,若A升高到T+△TA,B升高到T+△TB,已知VA=3VB,要使水银保持不动,则( )
如图所示,两容器用水平细管相连,容器内充有温度为T的同种气体被一小段水银隔成A、B两部分,现使A、B同时升高温度,若A升高到T+△TA,B升高到T+△TB,已知VA=3VB,要使水银保持不动,则( )
 如图所示,两容器用水平细管相连,容器内充有温度为T的同种气体被一小段水银隔成A、B两部分,现使A、B同时升高温度,若A升高到T+△TA,B升高到T+△TB,已知VA=3VB,要使水银保持不动,则( )
如图所示,两容器用水平细管相连,容器内充有温度为T的同种气体被一小段水银隔成A、B两部分,现使A、B同时升高温度,若A升高到T+△TA,B升高到T+△TB,已知VA=3VB,要使水银保持不动,则( )| A. | △TA=2△TB | B. | △TA=△TB | C. | △TA=$\frac{1}{2}$△TB | D. | △TA=$\frac{1}{4}$△TB |
1. 空气能热水器采用“逆卡诺”原理,工作过程与空调相反,能将空气中免费热量搬到水中进行制热,即使在南极也有良好表现,高效节能,是广东在世界领先的核心技术.如图,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A. 其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换).该循环过程中,下列说法正确的是( )
空气能热水器采用“逆卡诺”原理,工作过程与空调相反,能将空气中免费热量搬到水中进行制热,即使在南极也有良好表现,高效节能,是广东在世界领先的核心技术.如图,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A. 其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换).该循环过程中,下列说法正确的是( )
 空气能热水器采用“逆卡诺”原理,工作过程与空调相反,能将空气中免费热量搬到水中进行制热,即使在南极也有良好表现,高效节能,是广东在世界领先的核心技术.如图,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A. 其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换).该循环过程中,下列说法正确的是( )
空气能热水器采用“逆卡诺”原理,工作过程与空调相反,能将空气中免费热量搬到水中进行制热,即使在南极也有良好表现,高效节能,是广东在世界领先的核心技术.如图,一定质量的理想气体从状态A依次经过状态B、C和D后再回到状态A. 其中,A→B和C→D为等温过程,B→C和D→A为绝热过程(气体与外界无热量交换).该循环过程中,下列说法正确的是( )| A. | 在B→C过程,外界对气体做正功 | |
| B. | 在A→B过程,气体从外界空气里吸收大量热能 | |
| C. | 在C→D过程,气体分子的平均动能不变 | |
| D. | 在D→A过程,单位时间内碰撞单位面积器壁的分子数减少 |
19.静止在地球上的物体都要随地球一起转动,关于物体与地球的下列物理量中,相同的是( )
| A. | 周期 | B. | 线速度 | C. | 转动半径 | D. | 向心加速度 |
 如图所示,在平面直角坐标系xOy的第二象限内有场强大小为E、沿x轴正方向的匀强电场,在第一象限内有一磁感应强度为B的圆形匀强磁场区域(图中未画出),磁场方向垂直xOy平面,圆形匀强磁场区域的边界与x轴相切于点P.两个质子(质子质量m,电荷量q,不计重力)a、b以相等的速率沿不同方向从P点同时射入磁场区,其中a的速度方向沿y轴正方向,b的速度方向与x轴正方向的夹角θ=30°,a、b经过磁场后都垂直于y轴进入第二象限,a通过y轴上的点Q,OP=2OQ=2L,且a、b经过y轴的时间间隔为t0.求:
如图所示,在平面直角坐标系xOy的第二象限内有场强大小为E、沿x轴正方向的匀强电场,在第一象限内有一磁感应强度为B的圆形匀强磁场区域(图中未画出),磁场方向垂直xOy平面,圆形匀强磁场区域的边界与x轴相切于点P.两个质子(质子质量m,电荷量q,不计重力)a、b以相等的速率沿不同方向从P点同时射入磁场区,其中a的速度方向沿y轴正方向,b的速度方向与x轴正方向的夹角θ=30°,a、b经过磁场后都垂直于y轴进入第二象限,a通过y轴上的点Q,OP=2OQ=2L,且a、b经过y轴的时间间隔为t0.求: